Kegel online berechnen - Neues Programm fertig / Problem: Radius oder Höhe aus Mantelfläche und Volumen berechnen

Question

Das neue Programm zum Berechnen von Kegeln online ist fertig und steht zum Einsatz bereit.

Vorschau: https://www.matheretter.de/rechner/kegelvorschau.gif

Programm: https://www.matheretter.de/rechner/kegel

Screenshot:

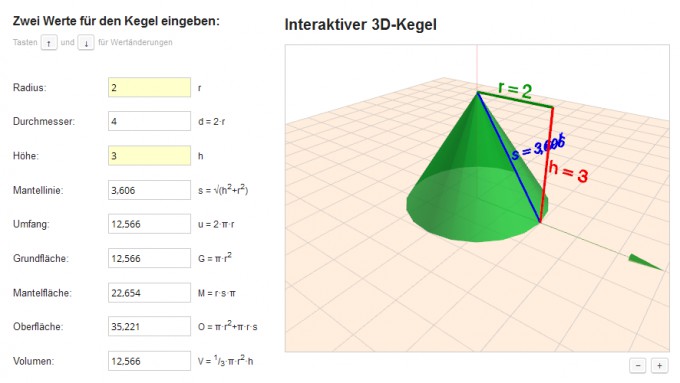
Das Programm kann alle Kegelwerte bestimmen. Dazu ermittelt es aus 2 gegebenen Werten stets Radius und Höhe.

Alle Wertkombinationen führen zu Radius und Höhe, nur die Höhe ist in drei Fällen nicht bestimmbar:

- Radius und Umfang
- Radius und Grundfläche
- Umfang und Grundfläche

Offenes Problem: Radius oder Höhe aus Mantelfläche und Volumen berechnen

Eine Berechnung steht noch aus, und zwar wenn Mantelfläche und Volumen gegeben sind. Die beiden Formeln lauten:

M = r·s·π

V = ¹/₃·π·r²·h

sowie die Mantellinie s = √(h²+r²)

1. Versuch: Radius bestimmen

s in M: M = r·√(h²+r²)·π

V nach h umgestellt:

h = 3·V / (π·r²)

h in M:

M = r·√( (3·V / (π·r²))²+r²)·π

Wolframalpha verrät uns 6 mögliche Ergebnisse, wobei 4 komplexe Zahlen enthalten, was die Berechnung erschwert.

2. Versuch: Höhe bestimmen

M = r·√(h²+r²)·π

V nach r² umgestellt:

r² = 3·V / (π·h)

r = √(3·V / (π·h))

r und r² in M:

M = √(3·V / (π·h))·√(h²+3·V / (π·h))·π

Auch hier gibt Wolframalpha Ergebnisse aus, die Komplexen Zahlen enthalten.

Vielleicht sieht jemand von euch noch eine weitere Herangehensweise?

Comments

Ich glaube, wenn man die Formel für M quadriert und entsprechend umformt, sollte es doch ohne komplexe Zahlen gehen:

M^2 = r^2 · s^2 · h^2

Einsetzen von s^2 = h^2 + r^2

M^2 = r^2 · (h^2 + r^2) · h^2

r^2 = 3·V / (π·h)

Damit

M^2 = (3·V / (π·h)) · (h^2 + (3·V / (π·h))) · h^2

https://www.wolframalpha.com/input/?i=M%C2%B2%3D3V%2F%28%CF%80h%29*%28h%C2%B2%2B3V%2F%28%CF%80h%29%29*h%C2%B2%2C+solve+for+h

---

Ich habe nunmehr die 3 Rechnungen eingebaut:

h₁ = - 3.√(-1/(3*PI)) * 3.√(PI²*M²-9*V²) / 3.√(V)

h₂ = 3.√(PI²*M²-9*V²) / ( 3.√(3*PI) * 3.√(V) )

h₃ = (-1)^{2/3} * 3.√(PI²*M²-9*V²) / ( 3.√(3*PI) * 3.√(V) )

wobei h₁ = h₃, sofern man ausnahmsweise (-1)^{2/3} = -1 setzt.

Interessant ist jedoch, dass die Ergebnisse nicht exakt sind:

Beispiel: https://www.matheretter.de/rechner/kegel?r=2&h=3 ergibt M=22,654 und V=12,566

Diese nunmehr eingesetzt: https://www.matheretter.de/rechner/kegel?v=12.566&m=22.654 ergeben r=1,957 (statt 2) und h=3,134 (statt 3). Hier kann ich noch nicht sagen, woher die Abweichungen kommen.

Auch Wolframalpha gibt diese Werte aus, Radius = 1,957.