Winkel-Bestimmung bei einem Punkt außerhalb eines Kreises bei gegebenem Radius und Sehne

Question

Gegeben sind ein Kreis vom Radius r und ein außerhalb dieses Kreises gelegener Punkt P.

Abbildung

Von P werden zwei Strahlen gezeichnet, die den Kreis in vier Punkten A, B, C und D so

schneiden, dass |AB| = |BC| = |CD| gilt.

Ein Strahl enthält die Punkte A und B, der andere die Punkte C und D. Dabei liegt der

Punkt D zwischen den Punkten P und C, und der Punkt A liegt zwischen den Punkten P

und B, siehe Abbildung

Man gebe eine allgemeine Formel zur Berechnung der Größe des Winkels APD in

Abhängigkeit von r und |AB| an.

Wie kann man daraus eine allgemeine Formel machen? Ich kenne dass nur wenn es tangenten sind

Comments

b) wie berechnet man genau den winkel bei r=3cm und AB = 5cm?

und ich muss diese Aufgaben nicht einreichen. Ich möchte nur Hilfe bei der Lösung, weil ich sonst keine bekomme...

---

Da Rätsel ich auch schon die ganze Nacht dran ? Hätte auch gerne einen Lösungsansatz

Answer 1

Schönen guten Morgen. Es bringt auch nichts sich in der Nacht zu quälen. Man sollte ausgeschlafen an die Aufgabe heran gehen.

Ich veredel mal die Skizze etwas

Ich denke alle eingezeichneten Winkel sind gleich groß und lassen lich mit dem Cosinussatz berechnen. Damit läßt sich auch der Winkel bei P bestimmen.

a^2 = r^2 + r^2 - 2*r^2*cos(α)
α = ACOS((2·r^2 - a^2)/(2·r^2)) <-- das hier ist der Mittelpunktswinkel im Kreismittelpunkt

APD = 2·ASIN((a^2 - 2·r^2)/(2·r^2))

Für a = 5 und r = 3 würde ich damit auf einen Winkel von 0.7989 oder 45.77° kommen.

Das sollte man von der Rechnung nochmal überprüfen und an einer Skizze kontrollieren. Diese Aufgabe überlasse ich euch aber gerne.

Comments

Elegant und auf den Punkte gebracht.

Stellt sich noch die Frage, wie du von:

α = ACOS((2·r² - a²)/(2·r²))

auf

∠APD = 2·ASIN((a² - 2·r²)/(2·r²))

gekommen bist.

---

α war der Mittelpunktswinkel. 

Also sind zwei Basis Winkel pi - α

Vier Basiswinkel sind also 2pi - 2α

Der Winkel bei P ist pi - (2pi - 2α) = pi - 2pi + 2α = 2α - pi = 2(α - pi/2)

Ersetzt man jetzt Alpha erhalten wir

2(ACOS(z) - pi/2) mit z = (2·r² - a²)/(2·r²)

Es gilt ACOS(z) = pi/2 - ASIN(z)

= 2(pi/2 - ASIN(z) - pi/2) 

= 2(- ASIN(z))

Es gilt -ASIN(z) = -ASIN(-z)

= 2·ASIN(- z) 

= 2·ASIN((a^2 - 2·r²)/(2·r²)) 

---

Die letzten Umrechnungen können natürlich auch weggelassen werden, sie dienen nur der Vereinfachung der Formel.

Answer 2

Aufgabe: Berechnung der Größe des Winkels APD in Abhängigkeit von r und |AB| an.

1. Als erster Schritt die anfänglichen Beschriftungen an der Figur:

 

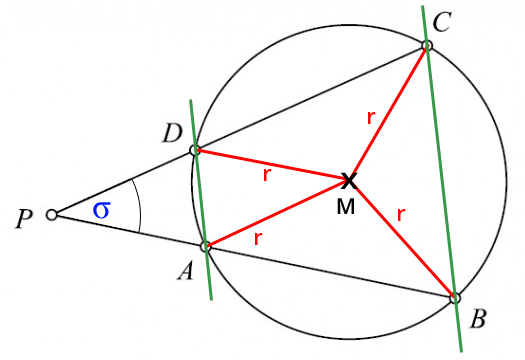
2. Dann folgen ein paar Formeln und wir tasten uns Schritt für Schritt an die Lösung heran:

Winkel im kleinen Dreieck ADP: σ = ∠APD, α = ∠DAP, δ = ∠PDA

Winkel im großen Dreieck BCP: σ = ∠BPC, β = ∠CBP, γ = ∠PCB

Winkel eingetragen:

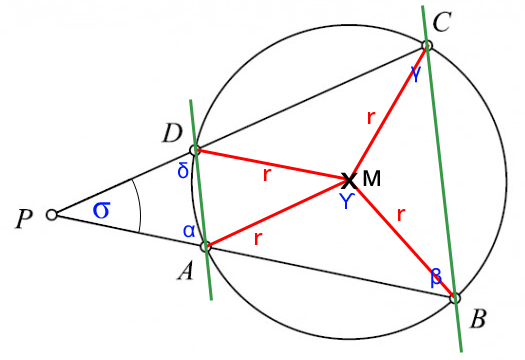
Um Winkel σ zu bestimmen, bieten sich Sinussatz und Kosinussatz an. 

Es ist festzustellen, dass das kleine Dreieck ADP dem großen Dreieck BCP ähnlich ist und damit folgende Winkel gleich sind: α = β und δ = γ. Unsere Abbildung ist aktualisiert:

 

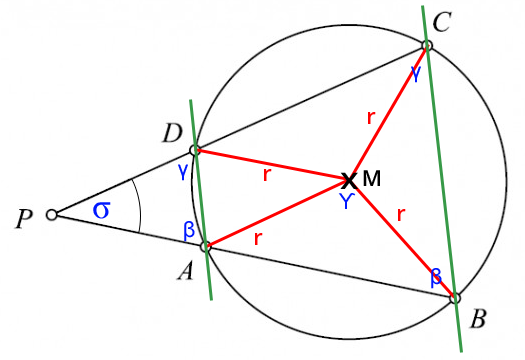
Sinussatz: AD / sin(σ) = DP / sin(β) = PA / sin(γ)

Sinussatz: BC / sin(σ) = CP / sin(β) = PB / sin(γ)

Kosinussatz: (AD)^2 = (PA)^2 + (DP)^2 - 2·(PA)·(DP)·cos(σ)

Kosinussatz mit r und AB, dann für Dreieck AMD:
(AB)^2 = r^2 + r^2 - 2·r·r·cos(ϒ)
(AB)^2 = 2·r^2 - 2·r^2·cos(ϒ)
(AB)^2 = 2·r^2 · (1 - cos(ϒ)) ← das ist die Formel für die Bestimmung der Basisseite im gleichschenkligen Dreieck

AMD ist ein gleichschenkliges Dreieck, genauso BMA, BCM und CDM. Damit kann man die allgemeine Formel zur Berechnung der Länge der Basis: c^2 = 2·a^2·(1-cos(ϒ)) verwenden. Für Dreieck BMA, das Strecke AB enthält, ergibt sich: (AB)^2 = 2·r^2·(1-cos(ϒ)), wobei ϒ = ∠AMB. Außerdem sind die Basiswinkel im gleichschenkligen Dreieck gleich groß.

Darüber hinaus sei darauf hingewiesen, dass AB die Sehne des Kreises ist und sich wie folgt berechnen lässt: s = 2·r·sin(α/2). Damit: AB = 2·r·sin(ϒ/2), wobei ϒ = ∠AMB.

---

Kommen wir zurück zur Formel der Länge der Basis und stellen diesen um nach ϒ:

(AB)^2 = 2·r^2 · (1 - cos(ϒ))
(AB)^2 / (2·r^2) = 1 - cos(ϒ)
(AB)^2 / (2·r^2) - 1 = -cos(ϒ)
-(AB)^2 / (2·r^2) + 1 = cos(ϒ)
arccos(-(AB)^2 / (2·r^2) + 1) = ϒ
ϒ = arccos(-(AB)^2 / (2·r^2) + 1)

---

Nun kommen wir auf die gegebene Information (hatte ich leider zu Beginn überlesen):

"dass |AB| = |BC| = |CD| gilt"



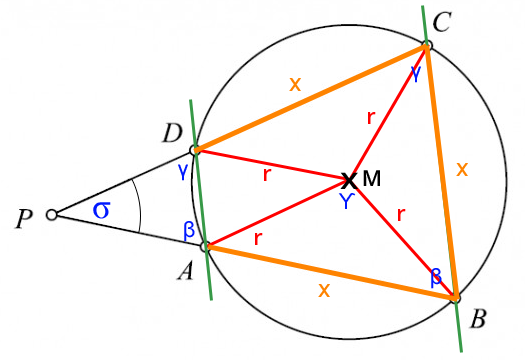
Mit dieser Angabe wird es einfach(er).

Betrachtet man nun die Dreiecke BMA, BCM und CDM stellt man fest, dass sie jeweils 2 Seiten haben, deren Länge r ist und eine Grundseite mit AB ("x" in der Abbildung). Das Dreieck AMD hingegen unterscheidet sich.

Nehmen wir zusätzlich den Strahlensatz:

PA / AB = PD / DC    | DC=AB

PA / AB = PD / AB    | *AB

PA = PD

Wir sehen, dass es sich beim Dreieck ADP auch um ein gleichschenkliges Dreieck handelt, damit sind die Basiswinkel β und γ gleich groß! Gleiches gilt für das ähnliche Dreieck BCP. → β = γ

Aktueller Stand:



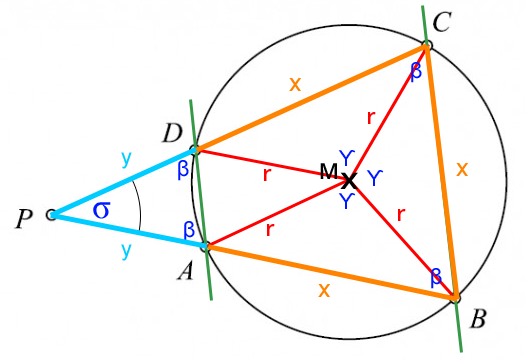
Winkel β ergibt sich aus zwei Basiswinkeln, siehe z. B. bei Punkt C, die gleichschenkligen Dreiecke treffen dort mit den gleichen Winkeln (nennen wir sie θ) zusammen:

β = 2·θ

// Winkelsummensatz Dreiecke: 180° = θ + θ + ϒ
180° = 2·θ + ϒ
θ = (180° - ϒ)/2  

β = 2·θ = 2·(180° - ϒ)/2  
β = (180° - ϒ)


Nun wieder den Winkelsummensatz anwenden für das große bzw. kleine Dreieck:

180° = σ + β + β
180° = σ + 2·β    | β = (180° - ϒ)
180° = σ + 2·(180° - ϒ)
180° = σ + 360° - 2·ϒ
σ = 180° - 360° + 2·ϒ
σ = 2·ϒ - 180°

Nun noch einsetzen, vgl. oben: ϒ = arccos(-(AB)^2 / (2·r^2) + 1)

Lösung:
σ = 2·arccos(-(AB)^2 / (2·r^2) + 1) - 180°

----

Einsetzen der Werte: r = 3 cm und AB = 5 cm

σ = 2·arccos(-(5)^2 / (2·3^2) + 1) - 180°
σ = 2·arccos(-25 / 18 + 1) - 180°
σ = 2·arccos(-25 / 18 + 1) - 180°
σ = 2·(112,885380476158569) - 180°
σ = 45,770760952317139°
σ ≈ 45,7707°