Seiten b, c und d in einem gleichschenkligen Trapez
Gesucht: b, c, d (b=d)
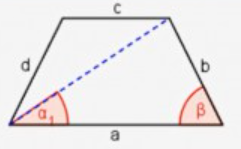
Gegeben:
a = 12 cm
α_{1} = 38°
β = 64°
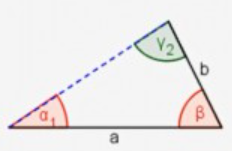
\( \gamma_{2}=180^{\circ}-38^{\circ}-64^{\circ}=78^{\circ} \)
\( \frac{b}{a}=\frac{\sin \alpha_{1}}{\sin \gamma_{2}} \quad \frac{b}{12 c m}=\frac{\sin 38^{\circ}}{\sin 78^{\circ}} \)
\( b = 7,6 \text{ cm} = d \)
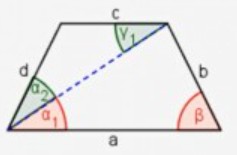
\( \alpha_{2}=\beta-\alpha_{1}=64^{\circ}-38^{\circ}=26^{\circ} \)
\( \gamma_{1}=\alpha_{1}=38^{\circ} \)
\( \frac{c}{d}=\frac{\sin \alpha_{2}}{\sin \gamma_{1}} \quad \frac{c}{7,6 \mathrm{~cm}}=\frac{\sin 26^{\circ}}{\sin 38^{\circ}} \)
\( c = 5,4 \text{ cm} \)
Nachtrag:
Ich suche die Seite a, wenn c gegeben wäre.