Gleichschenkliges Trapez mit AB als Durchmesser des Umkreises.

Question

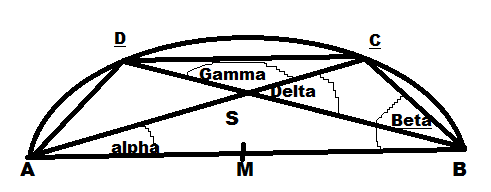
Aufgabe:

'Das Viereck ABCD ist ein gleichschenkliches Trapez, dessen Eckpunkte auf einem Kreis mit dem Durchmesser Strecke AB liegen. Es seien Strecke AB = 9 cm und Winkel alpha = 30 Grad.'

a) Bestimme mithilfe von Rechnungen die Größe der Winkel Beta, Gamma und Delta.

b) Bestimme die Länge der Strecke CD

c) Berechne den Umfang u und den Flächeninhalt A des Trapezes.

d) Zerlegen die Diagonalen das Trapez in ähnliche Dreiecke? Begründe die Antwort.

Comments

Sry,passt grad nicht zur Aufgabe.Aber wie hast du das Bild hochgeladen?

---

Habs mit Paint gemalt, gespeichert und hochgeladen ^^

Answer 1

Hier der Lösungsweg.

mfg Georg

Answer 2

Ich nehme an, die Skizze stammt von Dir,; sie verzerrt ein wenig die wesentlichen Aspekte. Wenn AB der Durchmesser des Kreises ist, gilt der Thalessatz und die Winkel ACB und ADB sind rechtwinklig.

Answer 3

Für β kann man den Thales zur Hilfe nehmen

β= 180-30-90=60

δ= 180-(60-30)-90=60

γ=180-δ=120

cos 30 *9= AC= 7,8

h= sin 30* 7,8= 3,9

CD = 9-2*(h/tan60)

Die Strecke CD ist 4,5.

BC= h/sin60=4,5.  BC=AD

U= 9+2*2,5+4,5=18

A=(9+4,5)/2. * 3,9=26,32

Comments

Fehlerhinweis
U= 9+2*2,5+4,5=18
U= 9+2*4,5+4,5=22.5 cm

---

Ja, klar , da habe ich wohl einen Übertragungsfehler gemacht.