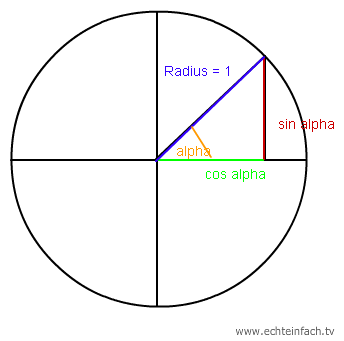
4.2 kann man am Einheitskreis zeigen. Dieser hat den Radius 1. Die rote Strecke ist der Sinus von Alpha, die grüne Strecke der Cosinus von Alpha. Nach dem Satz des Pythagoras gilt auch a^2 + b^2 = c^2, wobei a = cos(alpha) und b = sin(alpha) und die Hypotenuse ist der Radius, also c = 1. Setzt man das ein erhält man
a^2 + b^2 = c^2 => cos(alpha)^2 + sin(alpha)^2 = 1
zu 4.3) Der gesamte Flächeninhalt ist (a+b)(a+b) = (a+b)^2 = a^2 + 2ab + b^2
Ein Dreieck hat den Flächeninhalt (a*b)/2. Zieht man 4 mal den Flächeninhalt des Dreiecks von der gesamten Fläche ab, erhält man das Quadrat c^2 in der Mitte, also
c^2 = a^2 + 2ab + b^2 - 4*(a*b)/2 = a^2 + 2ab + b^2 -2ab = a^2 + b^2
=> der Satz des Pythagoras! c^2 = a^2 + b^2