Aufgabe 4 (Hauptachsentransformation):
Schreiben Sie die Kurve
\( x^{2}-4 x y+y^{2}+10 x+y+12=0 \)
als Matrixgleichung und berechnen Sie die Eigenwerte und normierten Eigenvektoren der Matrix.
Aufgabe 5 (Fortsetzung Aufgabe 4):
Führen Sie eine Drehung und anschließend mit der quadratischen Ergänzung entsprechend zur Vorlesung eine Verschiebung durch. Welchen Namen hat die Kurve (Ellipse, Hyperbel, Parabel, Geradenpaar)?
Aufgabe 6:
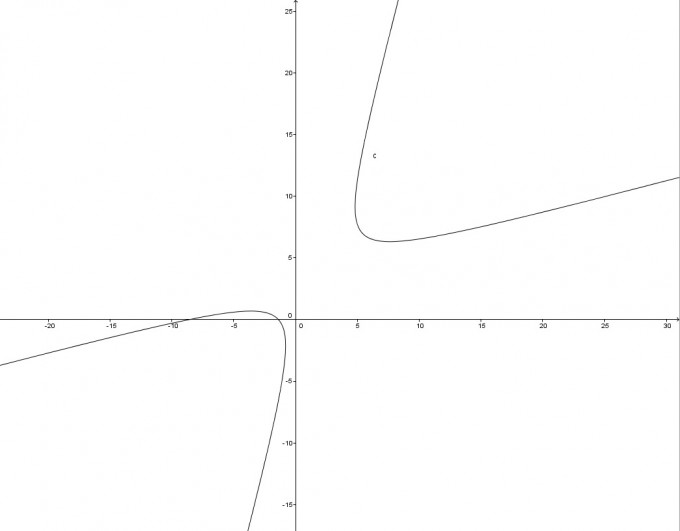
Skizzieren Sie die Kurve aus Aufgabe 4 und die in Aufgabe 5 durch die Hauptachsentransformation erhaltene Kurve. Verwenden Sie z.B. Maple.
Aufgabe 7:
Zeigen Sie, dass für die in den Aufgaben 4 und 5 berechneten Matrizen gilt: \( R^{T} A R=D \)
Meine Lösung zur Aufgabe 4:
\( x^{2}-4 x y+y^{2}+10 x+y+12=0 \)
\( \left(x_{1} y\right)\left(\begin{array}{cc}1 & -2 \\ -2 & 1\end{array}\right)\left(\begin{array}{l}x \\ y\end{array}\right)+(10,1)\left(\begin{array}{l}x \\ y\end{array}\right)+12=0 \)