In der Abbildung ist der Verlauf der Alkoholkonzentration im Blut nach einmaliger Einnahme verschiedener Alkoholmengen dargestellt.
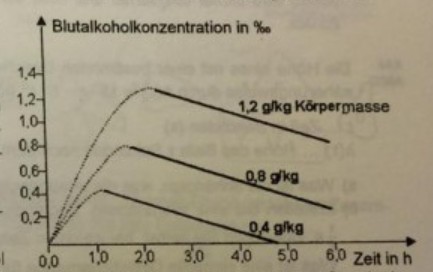
a) Vergleichen Sie die Verlaufe der Graphen in jenen Bereichen, in denen die Alkoholkonzentration zunimmt. Beschreiben Sie insbesondere, wann jeweils die höchste Konzentration erreicht ist.
b) Betrachten Sie den Graphen fur die einmalige Einnahme von \( 1,2 \mathrm{~g} \) Alkohol pro \( \mathrm{kg} \) Körpermasse.
Schätzen Sie, wann in diesem Fall kein Alkohol mehr im Blut vorhanden ist (vorausgesetzt der Abbau verläuft weiter so, wie in den ersten Stunden).
c) Begründen Sie, dass die pro Stunde abgebaute Alkoholkonzentration unabhängig von der eingenommenen Alkoholmenge ist.
Ermitteln Sie, wie viel Promille pro Stunde ca. abgebaut werden.
d) Im Internet findet man folgende Formel zur Berechnung der Alkoholmenge:
Getränkemenge in \( \mathrm{ml} \times( \) Vol.- \( \% / 100) \times 0,8= \) Gramm reiner Alkohol
Dabei ist Vol.-\% der Alkoholgehalt des Getranks in Volumenprozent.
Berechnen Sie anhand dieser Formel, wie viele ganze Flaschen Bier (330 ml, 4,8 Vol.-%) jemand trinken kann, wenn er nicht mehr als \( 40 \mathrm{~g} \) Alkohol zu sich nehmen möchte.