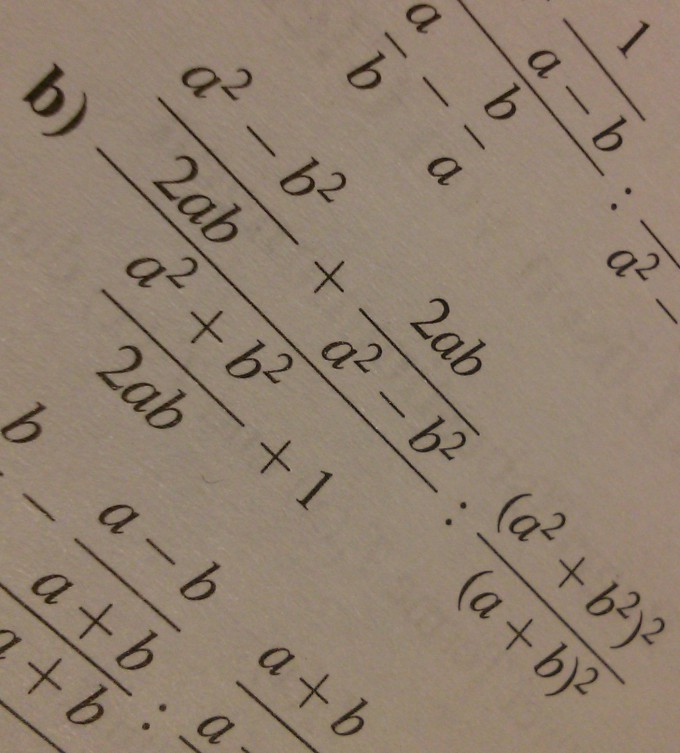Generelle Frage im Umgang mit komplizierten Mehrfach-Bruchaufgaben

Question

Angenommen ich habe mehrere Brüche in einer Aufgabe, wie beispielsweise hier... mir ist nicht ganz klar ob ich hier eine Reihefolge beachten muss?

{ [ ((a² - b²) / (2ab)) + ((2ab / (a² - b²)) ] / [ ((a² + b²) / (2ab)) + 1 ] } : [(a² + b²)² / (a + b)²]

Answer 1

Lautet der Term wie folgt

((a^2 - b^2)/(2·a·b) + 2·a·b/(a^2 - b^2)/((a^2 + b^2)/(2·a·b) + 1))/((a^2 + b^2)^2/(a + b)^2)

Generell wurde ich hier den zunächst mit dem rechten Doppelbruch im Zähler anfangen den auf einen Bruch zu bringen. Dann mit dem Bruch auf der linken Seite zu addieren und am Ende noch mit dem Kehrwert des unteren Bruches multiplizieren. Dabei lasse ich immer soviele Faktoren wie möglich stehen. Dann sieht man schnell was man kürzen kann. In der obigen Aufgabe habe ich aber vielleicht einen Interpretationsfehler drin, weil kein so schönes Ergebnis heraus kommt.

Comments

Mist, tut mir Leid... habe da irgendwo eine Klammer vergessen, habe nun mal ein Bild eingefügt, das ist leichter. ^^

Arbeite mich nach und nach durch den Gellrich hindurch aber bei solchen Aufgaben komme ich dann öfter mal ins Straucheln, weil ich z.B. dann mehr "ausrechne" und dann ein Chaos an hohen Potenzen erzeuge was ich dann nicht mehr so gut handhaben kann.

Meine Herangehensweise war folgendermaßen:

Ich habe erst einmal oben die Brüche gleichnamig gemacht und verrechnet, dann den untersten Bruch mit der + 1 ebenso. Dann habe ich den Kehrwert des rechten äußeren Bruchs multipliziert (also oberen Term des rechten Bruchs mit oberen linken Bruch multiplizieren und Nenner d. rechten Bruchs mit dem unteren Bruch im linken Nenner. (Hoffe das war jetzt nicht zu umständlich erklärt)

Irgendwo bau ich da aber immer einen Fehler ein... bei dem ich dann zu keinen schönen Ergebnissen komme, daher dachte ich meine Vorgehensweise wäre falsch.

Das Problem ist glaube ich in meinem Fall das Verständnis des Kommutativgesetzes, da x : y : z ja etwas unterschiedliches ist als y : z : x. Gilt dies bei solchen Ausdrücken auch? Mir war nun nicht ganz klar ob man generell erstmal den Linken Teil für sich ausrechnen muss (Nach Kommutativgesetz schon oder?) und dann erst den rechten "hineinzieht" oder ob es in dem Fall keine Rolle spielt... vielleicht könntest du mir das etwas näher bringen. :)

---

((a^2 + b^2)/(2·a·b) + 2·a·b/(a^2 - b^2))/((a^2 + b^2)/(2·a·b) + 1) : (a^2 + b^2)^2/(a + b)^2

Da komme ich jetzt auf 

= (a^4 + 4·a^2·b^2 - b^4) / ((a^2 - b^2)·(a^2 + b^2)^2)

---

1 / (a^2 - b^2) soll da angeblich rauskommen

---

Ja stimm,t. Ich hatte noch oben ein plus statt ein Minus drin.

((a^2 - b^2)/(2·a·b) + (2·a·b)/(a^2 - b^2))/((a^2 + b^2)/(2·a·b) + 1) : ((a^2 + b^2)^2/(a + b)^2)

Aber das Umformen kann ich hier mit meinen TEX Kenntnissen nicht machen.