Bernhard spielt an einem Abhang Golf (siehe untere Abbildungen) Die Flugbahn seines Balles wird durch die Funktion "f(x)=-1/100x² + x beschrieben. Der Verlauf des Abhangs kann in guter Näherung durch die Funktion g(x)= -2/5x beschrieben werden. x = Entfernung in Metern ; y=Höhe in Metern - jeweils vom Abschlagsort aus gemessen)
a) Berechne die Koordinaten des Auftreffpunktes Z.
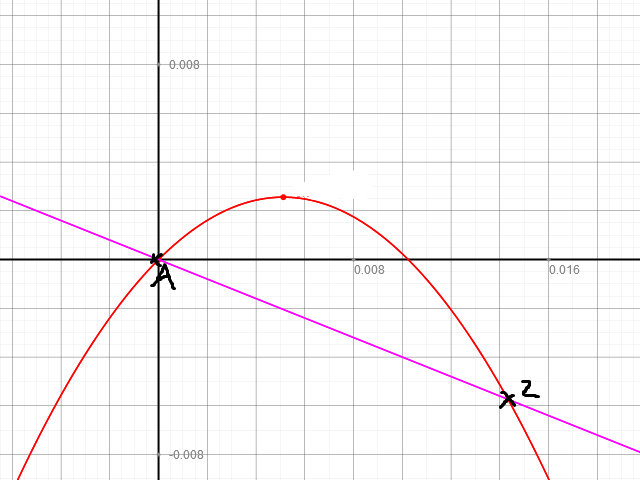
b) Zeiche Flugbahn und Abhang in ein Koordinatensystem.
c) Bestimme mit Hilfe deiner Zeichnung den Abstand zwischen A und Z
Haben wir zusammen an der Tafel gemacht. Wäre hilfreich wenn mir jemand sagen könnte was hier berechnet wurde Gleichsetzen:
\( -\frac{1}{100} x^{2}+x=-\frac{2}{5} x \quad \mid:\left(-\frac{1}{100}\right) \)
\( \begin{array}{lc}x^{2}-100 x=40 x & 1-40 x \\ x^{2}-140 x=0 & \text { | } q . E \\ x^{2}-140 x+4900= & 4900 \quad \mid T\end{array} \)
\( (x-70)^{2}=4900 \quad | \sqrt{ ~ } \)
\( x+70=70 \quad | -70 \)
\( x-70=70 \quad | +70 \)
\( x 1=0 \)
\( x 2=140 \)