Aufgabe 13:
Gegeben sind die Funktionen \( f \) und \( g \) mit \( f(x)=2 x \cdot e^{2-x} \) und \( g(x)=x^{2} \cdot e^{2-x} \)
In der Abbildung sind die zugehörigen Funktionsgraphen dargestellt.
a) Begründen Sie, warum \( \mathrm{G}_{\mathrm{f}} \) der Graph von \( \mathrm{f} \) und \( \mathrm{G}_{\mathrm{g}} \) der Graph von \( \mathrm{g} \) sein muss.
b) Untersuchen Sie, ob der Hochpunkt des Graphen von \( \mathrm{g} \) und der Wendepunkt des Graphen von \( f \) zusammenfallen.
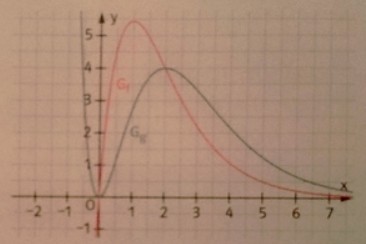
Abbildung aus "Lambacher Schweizer - Mathematik für Gymnasien [...] Qualifikationsphase Grundkurs", Klett-Verlag, S. 35
Aufgabe 14:
Eine Firma berechnet die täglichen Verkaufszahlen eines Handymodells, das neu eingeführt wird, modellhaft mit der Funktion \( f_{k} \) mit \( f_{k}(t)=k \cdot(t-15) \cdot e^{-0.01 t}+k \cdot 15 \quad(k>0 ; t \) Anzahl der Tage nach Einführung des neuen Modells).
a) Die Firma erwirtschaftet einen Gewinn, wenn täglich mehr als 4500 Handys verkauft werden. Berechnen Sie die Länge des Zeitraums, in dem ein Gewinn erwirtschaftet wird, für \( k=200 \).
b) Berechnen Sie für \( k=200 \) den Zeitpunkt, zu dem die tägliche Verkaufszahl maximal ist und geben Sie die maximale Verkaufszahl an.
c) Zeigen Sie, dass der Zeitpunkt, zu dem die Verkaufszahl maximal ist, unabhängig von \( k \) ist.
d) Zeigen Sie, dass der Modellfunktion \( f_{k} \) zufolge die Verkaufszahlen für alle \( k>0 \) ständig sinken, nachdem die maximale Verkaufszahl erreicht wurde.