Pythagoras: Fläche eines rechtwinkligen Dreiecks und Hypotenusenabschnitte.

Question

Ein rechtwinkliges Dreieck hat die Katheten a = 8 cm und b = 4 cm.

a) Berechne den Fächeninhalt des Dreiecks, die Hypotenuse c und daraus die Höhe h des Dreiecks.

b) Wie lang sind die beiden Abschnitte, in welche die Hypotenuse durch den Fußpunkt der Höhe h_{c} geteilt wird?

Der Lösung zufolge ist A = 16 cm².

Answer 1

eine kleine Skizze ist zumeist recht hilfreich:

 

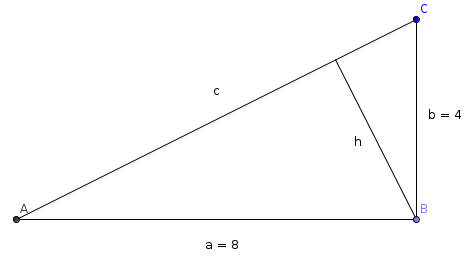
Wenn wir dieses Dreieck verdoppeln würden, hätten wir ein Rechteck mit den Seiten a = 8 und b = 4 und damit einen Flächeninhalt von A = 8cm * 4cm = 32cm²; wir verdoppeln aber nicht und kommen deshalb auf einen Flächeninhalt von 

A = 8cm * 4cm / 2 = 16cm²

Die Hypotenuse c berechnet sich nach Pythagoras wie folgt:

c² = 8² + 4² = 64 + 16 = 80

c = √(80cm²) ≈ 8,94cm

Nun könnten wir das Dreieck wieder verdoppeln, indem wir eine Parallele von c durch B ziehen und kämen auf den oben berechneten Flächeninhalt A = 32cm² ; diesmal mit den Seiten c und h; also

c * h = 32 | :c

h = 32/c = 32/√80 ≈ 3,58 (cm)

Besten Gruß

Comments

Wieso kann man eig für A nicht die Formel eines Dreiecks nehmen und nimmt die eines halben Rechtecks?:)

Danke :)

---

Natürlich kann man für A auch die Formel eines Dreiecks nehmen; das läuft ja auf dasselbe hinaus:

Ganz oben haben wir als Grundseite a = 8cm und als Höhe b = 4cm.

Damit kommen wir ebenfalls auf A = 8cm * 4cm / 2 = 16cm² 

Und ganz unten hatte ich die genannte Formel

h_c=(a*b)/c

nicht parat :-)

---

Achso weil es rechtwinklig ist!

Answer 2

Hi,

geg:

a= 8cm, b=4cm

ges:

c=?

a²+b²=c²

8²+4²=c²

64+16=c²

80=c²  |√

8,9=c

Also ist die Hypotenuse 8,9cm lang. Das ist ja auch so Richtig, denn die Hypotenuse ist immer die längste Seite am Rechwinkligen Dreieck

Nun die Höhe berechnen

h_c=(a*b)/c

h_c=(8*4)/8,9

h_c=3,6

Die Höhe des Dreicks ist also 3,6cm lang

Nun den Flächeninhalt

A=(a*b)/2

A=(8*4)/2

A=16cm²

Comments

Zur Kontrolle und etwas kürzer:

A = (a*b)/ 2 = (4*8)/2 cm^2 = 16 cm^2.

Grund: Rechtwinklige Dreiecke sind halbe Rechtecke.

Dein Rechenweg ist damit richtig, wenn auch etwas länger.