Parallele zur y-Achse

Question

ich habe eine Aufgabe, bei der ich leide nicht weiterkomme und wäre sehr dankbar, wenn mir da jemand helfen könnte.

Die Aufgabe lautet: Ermitteln Sie die Gleichungen einer Parallelen zur y-Achse, die den Flächeninhalt zwischen Graph von f und x-Achse über dem Intervall [0;2] halbiert. Gegeben ist die Funktion f(x)=3x²+2.

Kann mir das jemand vielleicht mit einem genauen Rechenweg erklären? Und wie würde das ganze aussehen bzw. was müsste man machen, wenn die Gleichung parallel zur x-Achse sein sollte?

Answer 1

f(x)=3x²+2.
∫ 3x² + 2 dx = 3*x³/3 + 2x
[ x³ + 2x ]₀²
2³ + 2*3 =  14 Flächeneinheiten

[ x³ + 2x ]₀^z  = 14 /2
z³ + 2*z = 7
Hier gibt es keine algebraische Lösung.
Es kann z.B. mit dem Newton Verfahren ermittelt werden
z = 1.57

Die Fläche wird durch eine Parallele zur y-Achse
bei x = 1.57 halbiert.

Ich gehe jetzt erst einmal fernsehschauen.

Deine andere Aufgabe ist lösbar aber wahrscheinlich
etwas komplizierter.
Ich schaue heute abend noch einmall rein.

Comments

Zurück vom fernsehen.

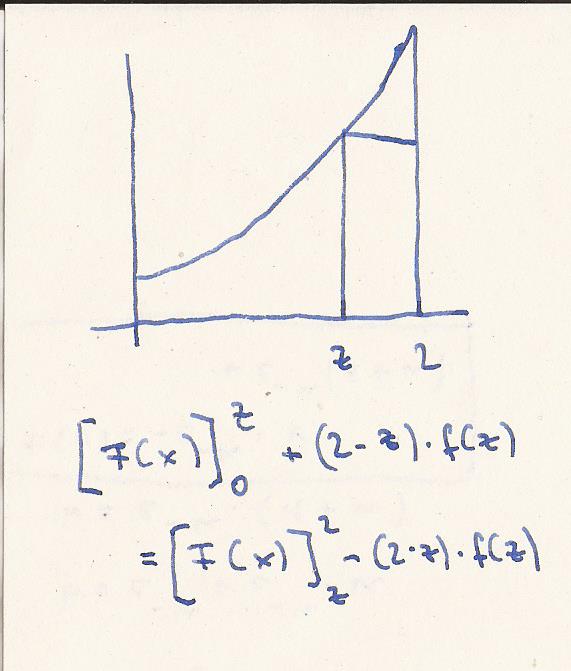
Die Skizze ist von den maßen nicht ganz glücklich gewählt.
Als prinzipielle Skizze aber richtig.

Die Parallele zur x-Achse welche die Kurve schneidet tut
dies im Punkt y = f ( z ).

F  ( x ) = Stammfunktion von f ( x ) = x³ + 2x

x = z ist der Punkt für den gilt :

Die Fläche links davon plus das Rechteck
( 2 - z ) * f ( z ) ist gleich
der Kurvenfläche rechts von z bis 2 minus
das Rechteck ( 2 - z ) * f ( z ).
Die beiden Flächen sollen gleich sein.

Schaffst du den Rest allein ?

Ansonsten bin ich bei Bedarf gern weiter behilflich.

mfg Georg