Was Akelei und Lu in ihren Antworten geschildert haben sind aber nur Spezialfälle des allgemeinen Falles einer beliebigen Strecke im freien Raum. Für diese kann man die Länge ebenfalls mit dem Satz des Pythagoras berechnen!
Sind die Begrenzungspunkte der Strecke P1(x1, y1, z1) und P2(x2,y2,z2), dann gilt für die Länge s der Strecke:
s2 = (x2-x1)2+(y2-y1)2+(z2-z1)2
Für die Herleitung denkt man sich einen Würfel, der die Strecke als Diagonale besitzt:
Als Beispiel hier eine Skizze für die Punkte
P1(0, 4, 2) und P2(6, 0, 0)
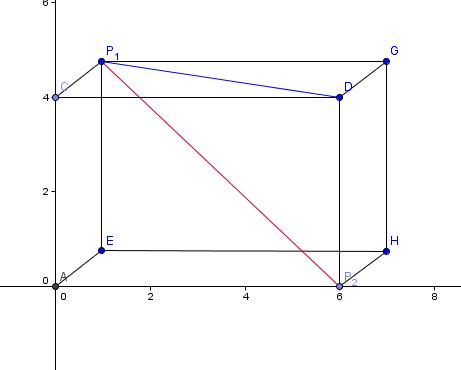
Der Quader hat die Seitenlängen a=6, b=4 und c=3.
Um die Länge s der roten Strecke zu berechnen, berechnet man zuerst die Länge r der blauen Strecke nach dem Satz des Pythagoras:
r2=a2+c2
Jetzt musst du beachten, dass die blaue Strecke gemeinsam mit der roten Strecke und der Strecke zwischen D und P2 ebenfalls ein rechtwinkliges Dreieck bildet!
Daraus folgt:
r2+b2=s2
r2 ist aber bereits von oben bekannt, somit folgt:
s2=a2+b2+c2,
was man auch als euklidischen Abstandsbegriff im Raum bezeichnet.
Hilfreiches Video hierzu: