analysisfrage kanalaufgabe schwer

Question

ein kanal der breite 10m knickt senkrecht in einen kanal der breite 5m ab. wie lang darf ein holzbalken mit vernachlässigbarer breite höchstens sein, damit er ohne zu verkanten schwimmend von der kanalströmung transportiert werden kann? kennt wer die lösung

Answer 1

Zunächst macht man sich eine kleine Skizze:

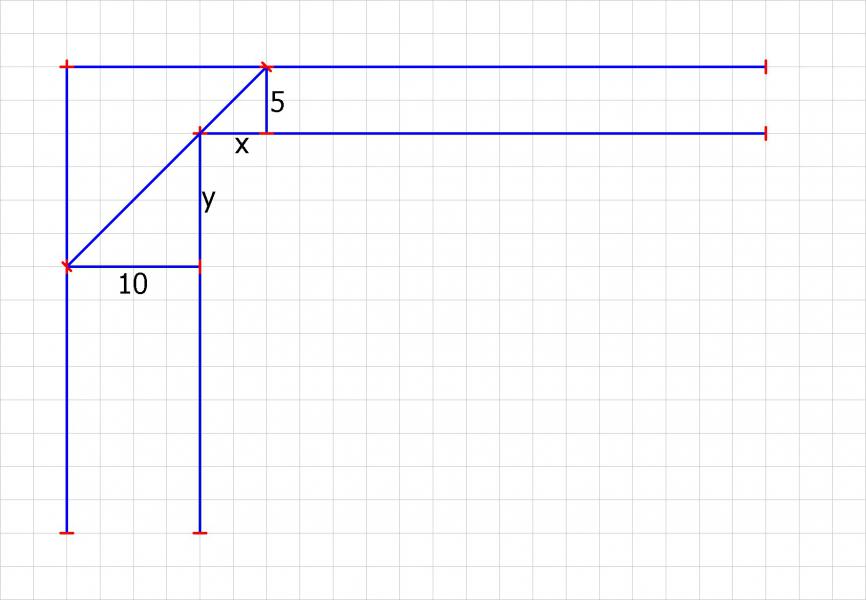
Nun stellt man die Hauptbedingung auf. Also die Streche die zu minimieren ist. Das ist hier die schräge Strecke, die den Balken darstellt.

Nach Phythagoras gilt:

s^2 = (x + 10)^2 + (y + 5)^2 = x^2 + 20·x + y^2 + 10·y + 125

Ungünstiger Weise treten hier 2 Unbekannte auf. Also brauchen wir eine Nebenbedingung um eine Variable durch eine andere Auszudrücken.

Da die beiden Dreiecke ähnlich sind gilt

5/x = y/10
y = 50/x

Jetzt kann ich also das y in der ersten Gleichung erstezen:

s^2 = x^2 + 20·x + (50/x)^2 + 10·(50/x) + 125 = x^2 + 20·x + 500/x + 2500/x^2 + 125

Wenn s Minimal wird wird auch s^2 minimal. Daher kann ich die Funktion ableiten und Null setzen

(s^2)' = 2·x - 500/x^2 - 5000/x^3 + 20 = 0
2·x^4 + 20·x^3 - 500·x - 5000 = 0

Eine Lösung finde ich für -10

(2x^4  + 20x^3  - 500x  - 5000) : (x + 10)  =  2x^3 - 500   
2x^4  + 20x^3                 
———————
- 500x  - 5000               
- 500x  - 5000               
———————
0

(x + 10) * (2x^3 - 500) = 0

Die weiteren Lösungen findet man also für 

2x^3 - 500 = 0
x = 250^{1/3} = 6.300

s^2 = (6.3)^2 + 20·(6.3) + 500/(6.3) + 2500/(6.3)^2 + 125 = 433.0
s = 20.81 m

Der Balken dürfte demnach höchstens 20.8 m lang sein.

Die Lösung kommt mir gerade etwas groß vor. Vielleicht könnte jemand duch eigene Rechnung das Ergebnis bestätigen oder widerlegen.

Answer 2

Skizze:

L = x + y
sin(w) = 10/x ⇔ x = 10/sin(w)
cos(w) = 5/y ⇔ y = 5/cos(w)
L(w) = 10/sin(w) + 5/cos(w)
L'(w) = -10cos(w)/sin²(w) + 5sin(w)/cos²(w)
L'(w) = 0 ⇔ sin³(w)/cos³(w) = 2 ⇔ tan³(w) = 2 ⇒ w = arctan(2^1/3).
L_max = 20,81
Habe also das gleiche Ergebnis.

Comments

Danke Danke für die schnelle hilfe