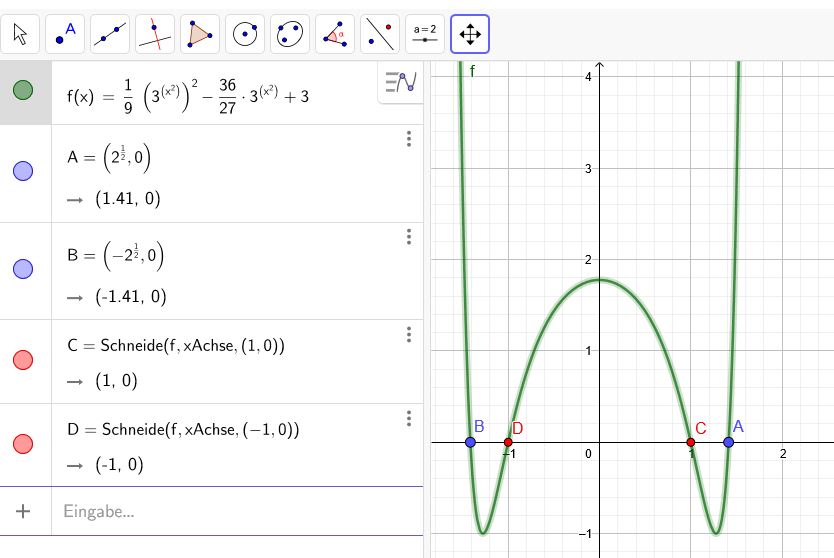
\( \frac{1}{9} \cdot (3^{x^2})^2-\frac{36}{27} \cdot 3^{x^2}+3=0|\cdot 9 \)
Lösung ohne Substitution:
\( (3^{x^2})^2-12 \cdot 3^{x^2}+27=0|-27\)
\( (3^{x^2})^2-12 \cdot 3^{x^2}= -27\)
\( (3^{x^2})^2-12 \cdot 3^{x^2}+(\frac{12}{2})^2= -27+(\frac{12}{2})^2\)
\( (3^{x^2}-6)^2=9|±\sqrt{~~}\)
1.)
\( 3^{x^2}-6=3\)
\( 3^{x^2}=9\)
\( 3^{x^2}=3^2\)
\(x^2=2\)
\(x_1=\sqrt{2}\)
\(x_2=-\sqrt{2}\)
2.)
\( 3^{x^2}-6=-3\)
\( 3^{x^2}=3\)
\( 3^{x^2}=3^1\)
\( x^2=1\)
\( x_3=1\)
\( x_4=-1\)
\(f(x)= \frac{1}{9} \cdot (3^{x^2})^2-\frac{36}{27} \cdot 3^{x^2}+3 \)