Lösungsweg ohne Substitution:
\( (e^x)^2-3e^{x}=-2 \)
\( e^{2x}-3e^{x}+(\frac{3}{2})^2=-2+(\frac{3}{2})^2=0,25 \)
\( (e^{x}-\frac{3}{2})^2=0,25 | \pm\sqrt{~~}\)
1.)
\(e^{x}-1,5=0,5 \)
\(e^{x}=2 \)
\(x \cdot \ln(e)=\ln(2) \) \( \ln(e)=1\)
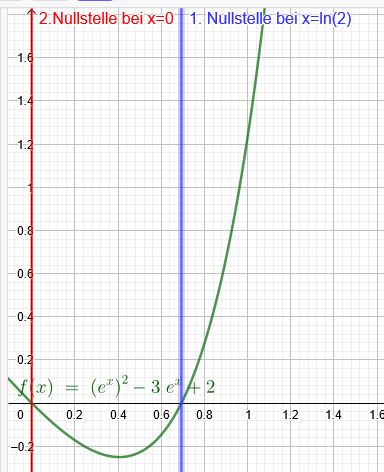
\(x_1=\ln(2) \)
2.)
\(e^{x}-1,5=-0,5 \)
\(e^{x}=1 \)
\(x_2=0 \)