Aufgabe:
Folgende Aufgabe:
Die Lösung müsste a=2 sein.
Ich komme allerdings mit meinem Lösungsweg nur auf a=0. Meines Wissens nach müsste die Determinante nämlich =0 sein damit das LGS keine eindeutige Lösung hat. Berechne ich allerdings die Determinante und forme nach a um erhalte ich nur a=0. 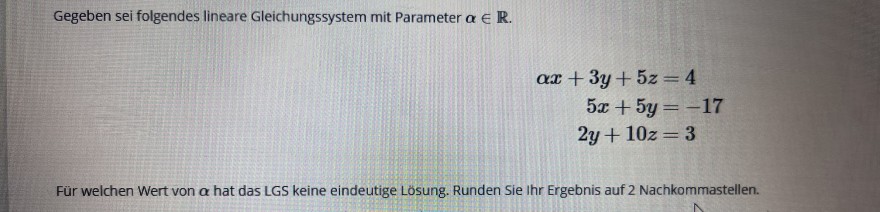
Text erkannt:
Gegeben sei folgendes lineare Gleichungssystem mit Parameter \( \alpha \in \mathbb{R} \).
\( \begin{aligned} \alpha x+3 y+5 z & =4 \\ 5 x+5 y & =-17 \\ 2 y+10 z & =3 \end{aligned} \)
Für welchen Wert von \( \alpha \) hat das LGS keine eindeutige Lösung. Runden Sie Ihr Ergebnis auf 2 Nachkommastellen.