Stecke mitten in der Klausurvorbereitung und brauche Hilfe bei der Rekonstruktion einer Funktion.

Question

Aufgabe: 

- ganzrationale Funktion 3-grades

-Extrema 1 : E(0/0)

-Extrema 2: E(2/4)

Answer 1

es ergibt sich:

f(0)=0

f'(0)=0

f(2)=4

f'(2)=0

und damit:

d = 0

c = 0

8a + 4b + 2c + d = 4

12a + 4b + c = 0

Also: f(x) = -x^3 + 3x^2

Grüße

Answer 2

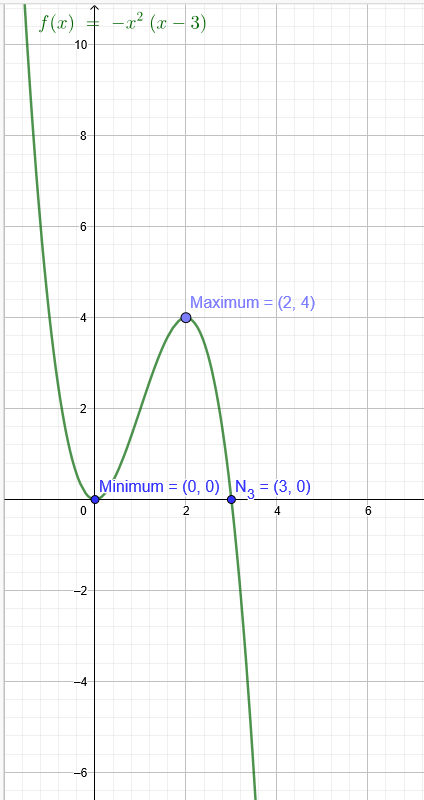
- ganzrationale Funktion 3-Grades     -Extrema 1 : E(0|0)         -Extrema 2: E(2|4)

Lösung über die Nullstellenform der kubischen Parabel:

f(x)=a*(x-N_1)*(x-N_2)*(x-N_3)

-Extrema 1 : E(0|0)   →  doppelte Nullstelle:

f(x)=a*x^2*(x-N_3)

E(2|4) liegt auf der Parabel:

f(2)=4a*(2-N_3)

4a*(2-N_3)=4   →a = \( \frac{1}{2-N_3} \)  

f(x)=\( \frac{1}{2-N_3} \)  *x^2*(x-N_3)

Extremwerteigenschaft : f´(x)=0

f´(x)=\( \frac{1}{2-N_3} \)  *[2x*(x-N_3)+x^2*1]

f´(2)=\( \frac{1}{2-N_3} \)  *[4*(2-N_3)+4]

\( \frac{1}{2-N_3} \)  *[4*(2-N_3)+4]

[4*(2-N_3)+4]=0

N_3=3         a = \( \frac{1}{2-3} \)  = - 1

f(x)=-x^2*(x-3)

Text erkannt:

4

Comments

@Moliets: die Frage ist über 6 Jahre alt ...

---

Das ist mir klar, aber vielleicht hilft der Weg ja dem einen oder der anderen.