Logische Verknüpfung (Aussagenlogik) ausdrücken durch d(A,B,C) = (A AND (NOT B) OR …)

Question

 Ich habe eine Frage für euch, hoffentlich könnt ihr mir helfen...

Wir betrachten folgende logische Verknüpfung von drei Aussagen A, B, C:

$$ d ( A , B , C ) = _ { d e f } ( A \wedge \neg B ) \vee ( A \wedge \neg C ) \vee ( \neg B \wedge \neg C ) $$

Drücken Sie folgende Aussagen logisch äquivalent ausschließlich mit Hilfe von d aus:

a) ¬ A

b) A

c) A ∧ B, wobei Sie zusätzlich die Konstante w verwenden dürfen

d) A ⊕ B(Antivalenz), wobei Sie zusätzlich die Konstante w verwenden dürfen

e) A  ⇔ B(Äquivalenz), wobei Sie zusätzlich die Konstante w verwenden dürfen
Hinweis: Sie dürfen beliebige Elementaraussagen einführen, identifizieren, vertauschen und Verknüpfungen
mit d ineinandersetzen. Sie dürfen also nur Aussagen der Form wie beispielsweise
d(d(C, A,B), d(A,D,B),B) bilden.

Answer 1

Habe einfach mal d(A,A,A) berechnet. Da bekomme ich

(A AND (NOT A)) OR (A AND (NOT A)) OR ((NOT A) AND (NOT A))

= ∅  OR ∅ OR (NOT A)

= NOT A

Also ist d(A,A,A) = NOT A. Also gerade Aufgabe a).

b) d(NOT A, NOT A, NOT A), ob das die Fragestellung erlaubt, ist unklar.

Vielleicht besser:  d(d(A,A,A),d(A,A,A),d(A,A,A)) = d( NOT A, NOT A, NOT A) = A
d darf ja gemäss Hinweis geschachtelt werden.

c), d)… Du musst vermutlich einfach pröbeln, bis es zufällig passt.

Vielleicht d(A,A,B) oder d(B,A,B)…

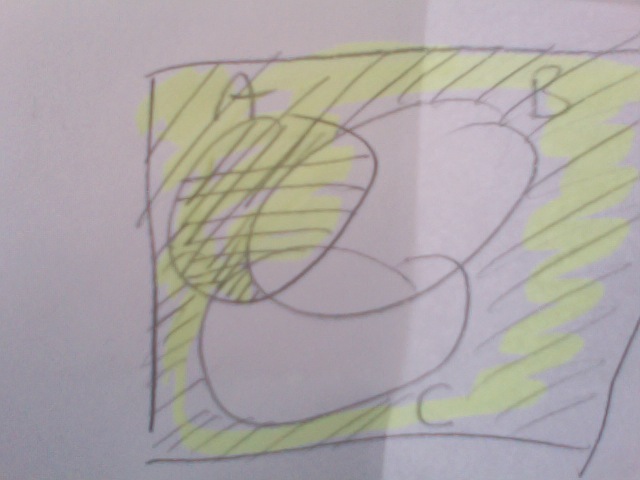
Hier noch eine graphische Darstellung von d(A,B,C). Vielleicht kannst du die brauchen, um systematisch zu raten.