Aufgabe:
Die Elektronikfirma stellt einen mp3-Player her. In der Abbildung ist die Anzahl der täglich verkauften mp3-Player im Verlauf eines Jahres dargestellt. Zur Vereinfachung der Modellierung wird im Folgenden mit einem Jahr mit 360 Tagen und einer konstanten Monatslänge von 30 Tagen gerechnet.
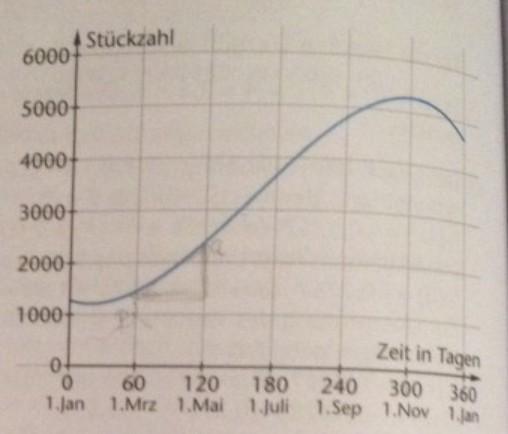
a) Entnehmen Sie die in diesem Aufgabenteil benötigten Informationen der Abbildung.
(1) Bestimmen Sie, wie viele mp3-Player ungefähr am 1. März verkauft wurden.
(2) Bestimmen Sie die mittlere tägliche Zunahme der Anzahl der täglich verkauf. ten mp3-Player für den Zeitraum vom 1. März bis zum 1. Mai.
(3) Ermitteln Sie, wie groß die momentane tägliche Zunahme der Anzahl der verkauften mp3-Player am 1. März war.
b) Anhand einiger Unternehmensdaten soll ein mathematisches Modell für die Anzahl der täglich verkauften mp3-Player erstellt werden:
- Am 1. Januar \( (t=0) \) wurden 1280 und am 1. September \( (t=240) \) wurden \( 4800 \) mp3-Player verkauft.
- Am 20. Januar \( (t=20) \) wurden die wenigsten mp3-Player verkauft.
- Die momentane Zunahme der verkauften mp3-Player betrug am 1. Mai \( (t=120) \) 20 Stück je Tag
(1) Stellen Sie anhand dieser Daten ein Gleichungssystem zur Bestimmung einer geeigneten ganzrationalen Funktion 3. Grades auf.
(2) Zeigen Sie, dass folgende Funktion \( f \) diese Bedingungen erfüllt:
\( f(t)=-\frac{10}{30} t^{3}+\frac{40}{15^{2}} t^{2}-\frac{20}{3} t+1280 \)
c) Nun sei durch \( f(t)=-\frac{10}{30} t^{3}+\frac{40}{15} t^{2}-\frac{20}{3} t+1280 \) eine Funktion zur Beschreibung der pro Tag verkauften mp3-Player gegeben. Dabei wird die Zeit \( t \) in Tagen und die Anzahl \( f(t) \) in Stück angegeben.
(1) Untersuchen Sie rechnerisch, wie viele mp3-Player nach diesem Modell maximal pro Tag verkauft wurden. Geben Sie an, wann dies der Fall war,
(2) Untersuchen Sie rechnerisch, wann die Zunahme der täglich verkauften mp3-Player am größten war,
(3) Berechnen Sie, wie viele mp3-Player im ganzen Jahr verkauft wurden,
d) Für das folgende Geschäftsjahr mit \( 360 \leq t \leqslant 720 \) nimmt die Unternehmensleitung an, dass die Verkaufszahlen exponentiell abnehmen werden. Zur Untersuchung von Prognosen wird dazu die Funktion g mit \( g(t)=a \cdot e^{-b}·t \) \( (a>0, b>0) \) so bestimmt, dass die Graphen von \( f \) und \( g \) an der Stelle \( t=360 \) ohne Sprung und ohne Knick aneinander anschließen.
(1) Bestimmen Sie die Koeffizienten a und b, so dass die obige Bedingung erfüllt ist.
(2) Berechnen Sie die mittlere Anzahl der in diesem Jahr täglich verkauften mp3-Player.
Ansatz/Problem:
Also an sich bin ich mit dieser Aufgabe gut klargekommen. Es gibt lediglich Probleme bei : a) (3) Ich weiss, dass damit die Steigung gemeint ist, aber dort kam das gleich wie bei a) (2) raus Und das ist falsch. Dann noch bei c) (2) den wendepunkt bei t=160 habe ich aber es steht in der Lösung, dass am 10. Juni die Zunahme für t=160 maximal war. Wie kommt man auf 10. Juni?