Am besten wäre es natürlich Du präsentierst Deine Lösung (auch gerne als Bild) damit wir Deine Problemstellen erkennen...
f(x)=x2+5x-3 g(x)=x-3
Bestimmen der Schnittpunkte:
f(x)=g(x)
x2+5x-3=x-3 |+3-x
x2+4x=0
x(x+4)=0 |Produkt ist dann Null, wenn es mindestens ein Faktor ist. ->
x1=0 und x2=-4
Nun noch in zum Beispiel in die Gerade g einsetzen -> y1=0-3=-3 und y2=-4-3=-7
Die Schnittpunkte sind also bei S1(0|-3) und S2(-4|-7) zu finden. Das hast Du sicher auch?
Kontrolle durch Schaubild:
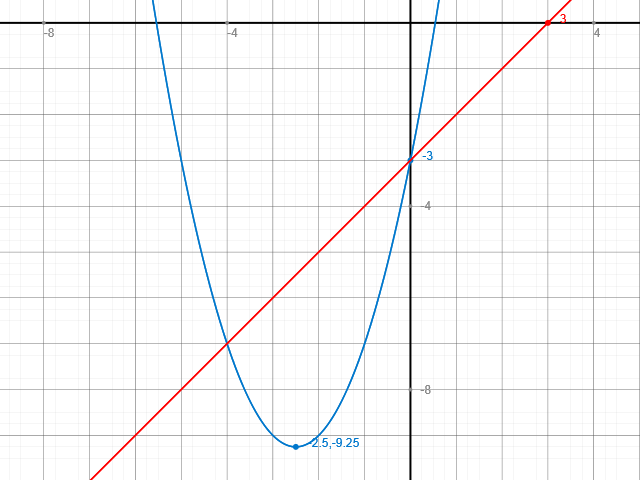
Passt also offensichtlich.
Zur Bestimung der Länge. Du hast Dir sicherlich schon ein "Steigungsdreieck" eingezeichnet, welches an der Geraden anliegt und von einem Schnittpunkt zum anderen geht. Da haben wir also ein rechtwinkliges Dreieck und können die Hypotenuse mittels Pythagoras bestimmen:
Kathete 1 hat die Länge 4 (die Differenz der x-Werte)
Kathete 2 hat die Länge 4 (die Differenz der y-Werte)
Abstand A=√(42+42)=√32≈5,66.
Wir haben also einen Abstand von 5,66 cm ;).