Aufgabe:
Die Graphen der reellen Funktionen \( \mathrm{p} \) und \( \mathrm{q} \) mit \( p(x)=-x^{2}+4 \) und \( q(x)=\frac{1}{2} x^{2}-2 \) und mit \( D_{p}=D_{q}=[-2 ; 2] \) bilden die abgebildete Fläche. Darin einbeschrieben ist das Rechteck ABCD, dessen Eckpunkte auf den Graphen der Funktionen \( \mathrm{p} \) und \( \mathrm{q} \) liegen.
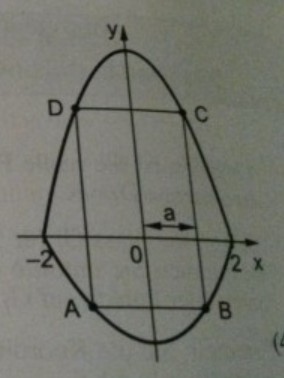
Bestimmen Sie die Maßzahl A(a) der Fläche des Rechtecks in Abhängigkeit von a und geben Sie eine sinnvolle maximale Definitionsmenge \( D_{A} \) an.
[Mögliches Teilergebnis: \( \left.\mathrm{A}(\mathrm{a})=-3 \mathrm{a}^{3}+12 \mathrm{a}\right] \)
Bestimmen Sie a so, dass die zugehörige Fläche maximalen Inhalt annimmt. Berechnen Sie für diesen Fall die Maßzahlen für die Fläche, Breite und Länge.
Ansatz/Problem:
Die Flächenfunktion lautet: A(a)=2a*(p(a)-q(a))
Wie komme ich auf p(a)-q(a)?
2a ist mir klar, aber dass ich für die Höhe des Rechteckes p(a)-q(a) einsetzen muss, verstehe ich nicht ganz.