Geometrische Bedeutung der Ableitung. Vergleich f(x) und f '(x) und f(x) = 1/x^2 ableiten

Question

ich hätte ein paar Fragen:

1. Könnt ihr mir die geometrische Bedeutung des Wertes der Ableitung einer Funktion an einer Stelle x₀ erläutern

2. Könntet ihr mir eine Skizze zur Funktion f(x) und f´(x) zeigen, so zum vergleichen wobei sich die zwei Funktionen unterscheiden und vielleicht erklären.

3.Und eine ausführliche rechnung f´(x) bestimmen: 

                 a)           f(x)=   √ (x+3)

                 b)           f(x)=  1/x²

 

Comments

Meinst du f(x)=   √ x+3 oder f(x)=   √ (x+3)   ?

D.h. steht 3 unter der Wurzel?

---

Ja die 3 steht unter der Wurzel, sry

Answer 1

1.) Die Ableitung einer Funktion f an der Stelle x₀ gibt die Steigung von f an dieser Stelle an bzw. die Steigung einer Tangenten an dieser Stelle.
Wenn der Wert der Funktion bei steigendem x wächst, dann ist die Ableitung positiv, umgekehrt ist sie negativ, wenn die Funktion fällt.

2.) Am Besten sieht man die einzelnen Details, wenn man sich eine eher komplizierte Funktion anschaut:

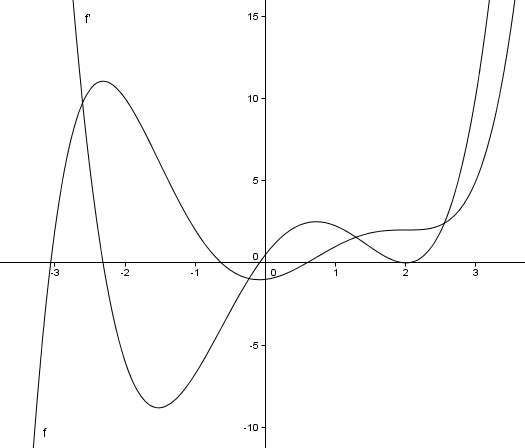
Folgende Punkte sind sehr charakteristischt:

x = 2: hier hat die Ableitung eine Nullstelle, damit ist die Tangente an f eine konstante Funktion: f hat ein Extremum, in diesem Fall ein Maximum.

x ≈  -1.5: hier hat die Ableitung ein Minimum, das ist also der Punkt, in dem f am stärksten fällt.

x ≈ - 0.1: hier hat die Ableitung wieder eine Nullstelle, f also ein Extremum.

x ≈  0.5: hier hat die Ableitung wieder eine Nullstelle, f also ein Extremum.

x = 2: hier hat die Ableitung zwar eine Nullstelle, aber sie wechselt ihr Vorzeichen nicht! Darum hat f kein Extremum, sondern einen sogenannten Sattelpunkt.

 

3.) Hier kann man die Lösung mit Hilfe der Potenzregel bestimmen:

Für f(x) = xⁿ gilt f'(x) = n*x^n-1.
Damit erhält man:

a) f(x) = √(x+3) = (x+3)^1/2

f'(x) = 1/2 * (x+3)^{1/2 - 1} = 1/2 * (x+3)^-1/2 = 1/(2√(x+3))

Dabei verwendet man außerdem noch die Kettenregel, wobei dadurch kein zusätzlicher Faktor auftritt, weil x+3 abgeleitet 1 ergibt.

b) f(x) = 1/x^2 = x^{-2}

f'(x) = -2*x^{-2-1} = -2*x^{-3} = -2/x^3

Answer 2

1) Könnt ihr mir die geometrische Bedeutung des Wertes der Ableitung einer Funktion an einer Stelle x_{0 erläutern}

_{Die Ableitung ist die Steigung des Graphen an einer Stelle oder die Tangentensteigung der Tangente an den Graphen an der Stelle.}

3) Und eine ausführliche rechnung f´(x) bestimmen:

f(x) = √x + 3 = x^{1/2} + 3
f'(x) = 1/2 * x^{-1/2} = 1/(2√x)

f(x) = 1/x^2 = x^{-2}
f'(x) = -2*x^{-3} = -2/x^3

2)

 Könntet ihr mir eine Skizze zur Funktion f(x) und f´(x) zeigen, so zum vergleichen wobei sich die zwei Funktionen unterscheiden und vielleicht erklären.

Wo f' die Nullstellen hat hat f die Steigung Null. Das sind auch Extrempunkte oder Sattelpunkte.

Comments

Heisst es dann bei der 1) dass es an der stelle x₀ keine steigung gibt und die stelle geometrisch gesehen auf 0 liegt?

und bei 3) rechnen wir es anders  ich versteh nicht ganz wie du Sie gerechnet haben.

wir rechnen so (anderes Bsp.):   f(x)= x³+5x

P1(x1 I y1)             P2(x2 I y2)

P1(x I x³+5x)         P2( x+e  Ι (x+e)³+5(x+e))

m=y2-y1/x2-x1

    =e²+3x²+3ex+5

Answer 3

wir rechnen so (anderes Bsp.):   f(x)= x3+5x

P1(x1 I y1)             P2(x2 I y2)

P1(x I x3+5x)         P2( x+e  Ι (x+e)3+5(x+e))

m=y2-y1/x2-x1

    =e2+3x2+3ex+5

b)           f(x)=  1/x^2

P1(x1 I y1)             P2(x2 I y2)

P1(x I 1/x^2)         P2( x+e  Ι 1/(x+e)^2)

m=(y2-y1)/(x2-x1)                         Beachte: Klammern sind zwingend!

                                                |jetzt Doppelbruch

    = (1/ (x+e)^2  - 1/x^2) / e

                     |Zähler auf einen Bruchstrich, Nenner als Bruch

   = ( (x^2 - (x+e)^2) /x^2*(x+e)^2) / (e/1)

                  |Zähler vereinfachen; mit Kehrwert multiplizieren

= (x^2 - x^2 - 2ex -e^2 ) / (ex^2 (x+e)^2)

= ( - 2ex -e^2 ) / (ex^2 (x+e)^2)

                   |e kürzen

= (-2x - e) / (x^2(x+e)^2)

     |zwei Brüche draus machen

= -2x/ (x^2(x+e)^2)  - e/ (x^2 (x+e)^2)

= -2/ (x(x+e)^2)  - e/ (x^2(x+e)^2)

Limes e → 0, (falls x ≠ 0)

= -2/x^3 = -2 x^{-3}

Schön mit Doppelbrüchen und Limes kannst du das bestimmt auf dem Papier besser.

Nebenbemerkung: f(x) = 1/x^2 hat in x=0 eine Definitionslücke. Daher auch keine definierte Steigung. 

Du hast bereits gesehen, dass in den andern Lösungen einfach die Regel zur Ableitung von Potenzen benutzt wurde.       f(x) = x^n     → f ' (x) = n*x^{n-1}

Das klappt also auch, wenn n = -2 ist.

f(x) = x^{-2}, f ' (x) = -2 * x^{-2-1} = -2x^{-3} = -2/x^3

 

Comments

Du hast beim erweitern einen kleinen Fehler gemacht, folgendermaßen kommt man auch auf dieselbe Lösung, die wir alle schon gepostet haben:

Der Grenzwert ist natürlich nur dann richtig, wenn x ≠ 0 gilt.

---

f(x) = √(x+3)         definiert für x ≥ -3  

P1(x1 I y1)             P2(x2 I y2)

P1(x I  √(x+3))                P2( x+e  Ι √(x+e+3))

(y2-y1) / (x2 - x1)

         (√(x+e+3) - √(x+3)) / e

             |mit √ + √ erweitern (3. Binom, um Wurzeldifferenz wegzubringen

        = (x+e+3 -(x+3))/(e(√(x+e+3) + √(x+3))

        =    e/(e(√(x+e+3) + √(x+3))

        |mit e kürzen

         =    1/ (√(x+e+3) + √(x+3))

Limes e-----> 0

f ' (x) = 1/ (2√(x+3) ) = 1/2  * (x+3)^{-1/2}         gilt nur für x> -3

Somit wieder dasselbe wie mit den üblichen Formeln.