Beweise im Dreieck mit Strahlen

Question

Im Dreieck ABC sei M der Mittelpunkt der Seite AB. An den Strahl [AB wird in A der Winkel angetragen, an den Strahl [BA in B der Winkel MCB, dabei wird die Drehrichtung jeweils so gewählt, dass die freien Schenkel auf der gleichen Seite von AB wie der Punkt C liegen.

Beweise, dass sich die freien Schenkel auf der Geraden CM schneiden.

Diese Aufgabe hat mir mein Mathelehrer über die Ferien gegeben, nur ich habe keinen Ansatz. 

Comments

Weißt du dann inzwischen, wie diese Aufgabe geht?

Answer 1

Zunächst mal ist deine Aufgabenstellung so nicht komplett. Es ist schon wichtig zu Wissen wie die Abhängigkeit der Winkelgrößen ist. Eventuell verbergen sich wichtige Informationen hinter den Kästchen.

Hast du dir denn selber dazu schon eine Skizze gemacht?

Weiterhin ist die Aufgabe so unklar. Der Winkel ACM wird beispielsweise bei C abgetragen und läuft vom Schenkel CA gegen den Uhrzeigersinn zum Schenkel CM. Zumindest habe ich das so früher gelernt.

Comments

Die Kästchen sind das winkelzeichen: ∠ 

Skizze noch nicht weil ich die Aufgabe nicht verstehe

Answer 2

Die kann dir dein Mathelehrer nur gegeben haben, wenn du am Bundeswettbewerb Mathematik teil nimmst, das ist nämlich die dritte Aufgabe der ersten Runde ;)

Die Skizze ist folgende:

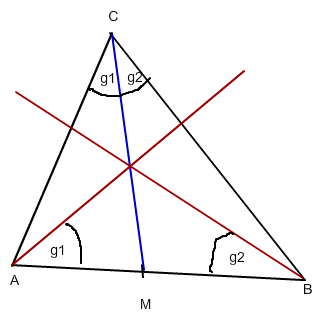
Dabei sollen g1 für Gamma 1 und g2 für Gamma 2 stehen.

nun habe ich es so gemacht:

Man nehme die Strecke AB als Basis. Der Punkt C sei der Schnittpunkt von den Strahlen, die von A und B ausgehen. Jetzt verschiebt man nur diesen Punkt, behält aber die Strecke AB bei. Irgendwann ist der Punkt C so verschoben, dass Die Winkel so groß sind wie ACM und BCM. 

Das ist aber vermutlich falsch, somit eine weitere Überlegung:

Eventuell sind die Dreiecke CM2S (M2 der Schnittpunkt der Seite AC und dem freien Schenkel) und AMS sowie die Dreiecke CM3S (M3 der Schnittpunkt der Seite BC mit freiem Schenkel) und BMS jeweils Abbildungen. Das heißt, das Dreieck AMS ist eine zentrische Streckung vom Dreieck CM2S und so weiter. Das müsste man jetzt nur noch zeigen, meine Idee wäre, dass man mit den Winkeln vom Schnittpunkt S argumentiert (Scheitelwinkel etc.), ich weiß nicht ob das stimmt und falls ja, mehr verrate ich nicht. Du musst beim BW der Mathematik nämlich angeben, dass du diese Aufgaben ALLEIN gelöst hast... 

Ich frage mich nur, wie man hier mit dem Strahlensatz arbeiten soll...geht zwar bei zentrischer Streckung, dazu muss man aber erstmal zeigen, dass eine vorliegt.