Hi,
die Fourierkoeffizienten kannst Du nach der Formel
$$ (1) \quad \gamma_k = \frac{1}{T} \int_{-\frac{T}{2}}^{\frac{T}{2}} f(\tau) e^{-i k \omega \tau} d\tau $$ für eine T-periodische Funktion berechnen.
Dabei ist in Deinem Fall \( T = 2 \) und \( \omega = \frac{2 \pi}{T} \)
Weil \( f(x) = f(-x) \) gilt, kann das Integral (1) wie folgt berechnet werden
$$ (2) \quad \gamma_k = \frac{1}{T} \int_{-\frac{T}{2}}^{0} f(-\tau) e^{-i k \omega \tau} d\tau + \frac{1}{T} \int_{0}^{\frac{T}{2}} f(\tau) e^{-i k \omega \tau} d\tau $$
und das ergibt
$$ \gamma_k = \frac{e^2 e^{-i \pi k} (2+i \pi k) + e^2 e^{i \pi k} (2-i \pi k) - 4}{2 \pi^2 k^2 +8} $$
Die Fourierapproximation lautet
$$ (3) \quad f(x) = \sum_{k=-\infty}^{\infty} \gamma_k e^{i k \omega t} $$
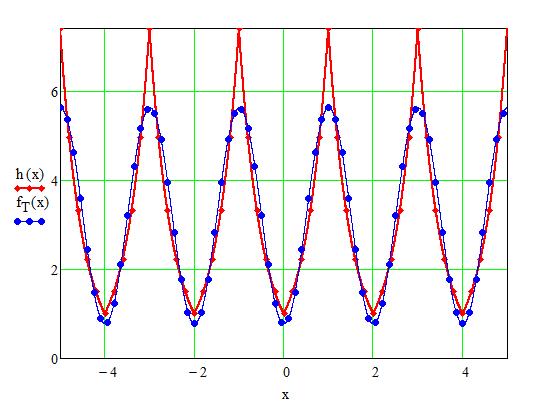
und für $$ f(x) = \sum_{k=-3}^{3} \gamma_k e^{i k \omega t} $$ siehst Du die Approximation im Bild unten