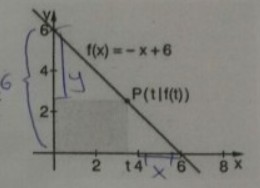Bestimme das Rechteck mit dem maximalen Flächeninhalt. (Extremalaufgabe)

Question

Aufgabe Funktionen und Ableitungen - Extremwertprobleme:

Rechtecke unter Funktionen

Es wird ein Rechteck untersucht, bei dem zwei Seiten auf den Koordinatenachsen liegen und ein Eckpunkt auf dem Funktionsgraph \( f(x)=-x+6 \). Bestimme das Rechteck mit dem maximalen Flächeninhalt.

Answer 1

f(x) = 6 - x

Die Fläche berechnet sich

A = x * f(x) = 6x - x^2

A' = 6 - 2x = 0 --> x = 3

Für x = 3 ist die Fläche am größten.

Answer 2

A=t*y

y=-t+6

A=t*(-t+6)

A(t)=-t²+6t

A´(t)=-2t+6 = 0

-2t+6=0

t=3

A´´(t)=-2    Also max.

A=3*(-3+6) = 9  (Max. Flächeninhalt)

LG