Winkelberechnung im rechtwinkligen Dreieck mit Höhe

Question

Im rechtwinkligen Dreieck mit den Katheten a und b ist a=6,3cm und c=9,7cm. Berechne den Flächeninhalt des Dreiecks.

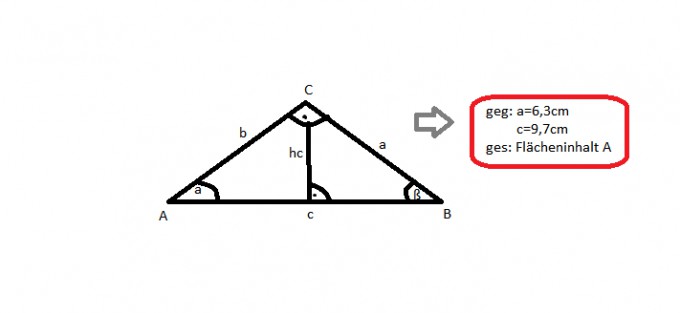Jetzt hat mir jemand den alpa WInkel mit cos(a) bestimmt, was ich absolut nicht nachvollziehen kann. Das einzig logische für mich wäre, den Winkel alpha durch sin(a)=a/c (also Gegenkathete durch Hypotenuse) zu bestimmen.

Noch etwas das ich nicht ganz nachvollziehen kann ist, wie bestimme ich die Seiten "a", "b" und "c", wenn nur der Winkel Beta (ß) und die Höhe (hc) angegeben sind, also wie genau geht man da vor, gibt es da irgendeine Formel oder herangehensweise für?

Comments

Meinst du hier? 

https://www.mathelounge.de/216514/winkelberechnung-im-rechtwinkligen-dreieck

Bitte Fragen nicht mehrfach einstellen.

Soll das ein gleichschenkliges Dreieck sein?

Warum rechnest du nicht so, wie es für dich logisch ist und schaust mal, was du rausbekommst?

---

Nein, laut der Aufgabenstellung, ist das kein gleichschenkliges Dreieck.

Allerdings ist die Aufgabe wo nur der Winkel Beta und die Höhe gegeben ist ein gleichschenkliges Dreieck...

---

Mit der ersten Aufgabe komme ich noch einigermaßen klar. Allerdings weiß ich nicht wo ich bei der zweiten Aufgabe ansetzen soll. Im gleichschenkligen Dreieck sind der Winkel Beta (ß) und die Höhe (hc) angegeben. Wie kriegt man da die Seiten "a","b" und "c" raus?

---

Die 3. Aufgabe habe ich dir im Link schon vorgerechnet.

Bei der 2. Aufgabe brauchst du die Höhe gar nicht. Vgl. Meine Rechnung unten.

Answer 1

EDIT: Tut mir leid! Zeilenumbrüche wollen nicht. Ich setze mal an jedes Zeilenende einen ; 

Im rechtwinkligen Dreieck mit den Katheten a und b ist a=6,3cm und c=9,7cm. Berechne den Flächeninhalt des Dreiecks.

Es gilt:

sin(A) = a/c = cos(B)     .  Von B aus gesehen ist a die Ankathete;    
  und  hc = a * sin(B)        | cos(B) einsetzen gemäss sin^2(B) + cos^{2}(B) = 1 ;  hc = a * √(1 - cos^2 B)   = a*√(1 - a^2 / c^2)  ; = a*√((c^2 - a^2)/c^2) ; = a*√(c^2 - a^2) / c  ;

  F = 1/2 * c * hc = 1/2 * c * a*√(c^2 - a^2)/c  ; = 1/2 a * √(c^2 - a^2)   ;
  Das stimmt schon, denn nach Pythagoras steht nun da  = 1/2 a*b   (halbes Rechteck!) Richtig!  ;
  Es ergibt sich aber sofort ein einfacherer Weg ;   
  F = 1/2 a*b (halbes Rechteck)  ;
  Pythagoras b = √(c^2 - a^2)  ;
  ==> F = 1/2 * a* √(c^2 - a^2) 

Comments

Danke für deine Hilfe