Aufgabe:
a) Modellieren Sie die Schulden der öffentlichen Haushalte durch exponentielles Wachstum.
b) Untersuchen Sie, wie gut Ihre Näherung ist, und geben Sie ggf. Gründe für Abweichungen an. Welche Prognose machen Sie für 2010? Wie groß ist nach Ihrem Modell die Verdoppelungszeit? Wie groß wären nach Ihrem Modell die Schulden im Jahre 1990 gewesen?
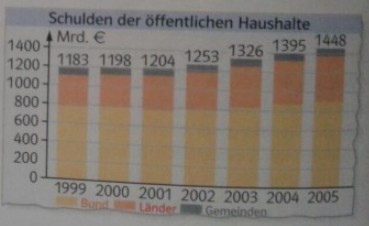
Schulden der offfentlichen Haushalte