In welchem Punkt ist die Tangente an den Graphen von f paralell zur Gerade?

Question

In welchem Punkt P (x0/f(x0)) ist die Tangente an den Graphen von f parallel zur Geraden g mit g(x)  = x-2?

f mit f(x)=x³

Answer 1

g(x) hat die Steigung m=1   Damit die Tang. in P die gleiche Steigung hat
muss also f ' (x) = 1 sein    da f ' (x) = 3x^2   also
                                                    3x^2 = 1
                                                        x = ±wurzel(1/3)   Also sogar zwei Punkte, bei
denen das der Fall ist.

Answer 2

In welchem Punkt P (x0/f(x0)) ist die Tangente an den Graphen
von f parallel zur Geraden g mit g(x)  = x-2?

f mit f(x)=x³

Die Gerade hat die Steigung 1
Die Tangente muß auch die Steigung haben
f ( x ) = x^3
f ´( x ) = 3 * x^2

3 * x^2 = 1
x^2 = 1/3
x = ± 0.5774
f ( ± 0.5774 ) = ( ± 0.5774 )^3 = 0.1925

( 0.5774  | 0.1925 )
( - 0.5774  | - 0.1925 )

Answer 3

f(x) = x³ 

f'(x) = 3x² | gibt die Steigung von f(x) an jedem beliebigen Punkt x an

g(x) = x - 2

g'(x) = 1 | gibt die Steigung von g(x) an jedem beliebigen Punkt x an

Gesucht ist also die Stelle x₀, an dem die Steigung von 3x² = 1 ist:

3x² = 1

x² = 1/3

x_1,2 = ± √(1/3)

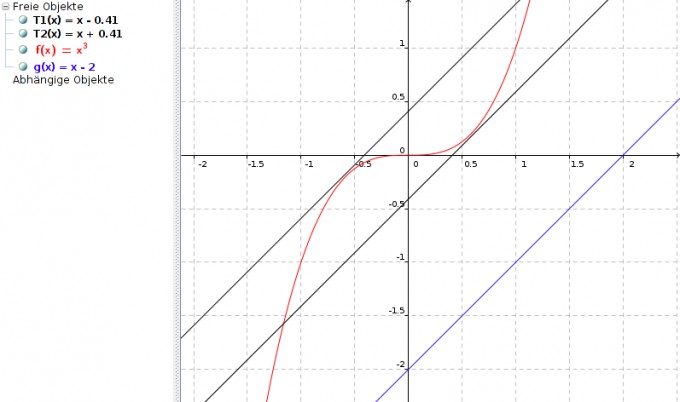
Es gibt also zwei Punkte, an denen die Steigung von f(x) = der Steigung von g(x) ist, die Tangente an f(x) also parallel zu g(x) ist:

P₁ (√(1/3)|(√(1/3)³) ≈ (0,577|0,192)

P₂ (-√(1/3)|(-√(1/3)³) ≈ (-0,577|-0,192)

 

Besten Gruß