Wahrscheinlichkeitsrechnen und Baumdiagramm Hilfe!

Question

Hallo vielleicht könnt ihr mir bei meiner Aufgabe hier helfen, ich komme schon lange nicht mehr weiter und weiß auch nicht so genau wie ich das mit dem Baumdiagramm machen soll.

Also hier die Aufgabenstellung:

Das Blut eines Menschen hat entweder die Eigenschaft Rhesus-positiv(RH+) oder Rhesus-negativ (RH-). Etwa 85% der Menschen sind RH+, die anderen RH. Wenn in einer Partnerschaft die Frau RH- ist und der Mann RH+, kann es bei einer Schwangerschaft ohne ärztliche Maßnahmen zu ernsten Komplikationen kommen. Wie wahrscheinlich ist die Kombination von Bluteigenschaften in einer Partnerschaft?

Ich habe bis jetzt es so gemacht die 85% :100= 17/20 und dann 15%:100= 3/20 in Bruch umgewandelt. was muss ich nun machen, zumal ich dass auch mit dem Baumdiagramm nicht verstehe.

Lg

Answer 1

ein Baumdiagramm dazu sieht in etwa so aus:

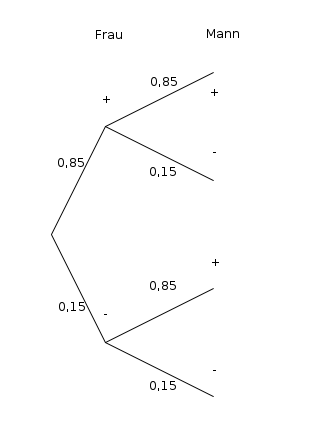
Die Wahrscheinlichkeiten entlang eines Pfades werden miteinander multipliziert:

P(Frau +, Mann +) = 0,85 * 0,85 = 0,7225 = 72,25%

P(Frau +, Mann - ) = 0,85 * 0,15 = 0,1275 = 12,75%

P(Frau -, Mann +) = 0,15 * 0,85 = 0,1275 = 12,75%

P(Frau -, Mann -) = 0,15 * 0,15 = 0,0225 = 2,25%

Die rot gekennzeichnete Kombination ist also die gefährliche, die mit einer Wahrscheinlichkeit von 12,75% auftritt.

Besten Gruß

Comments

Ahh jetzt ergibt das auch einen Sinn vielen Dank du warst mir eine große Hilfe!!

---

Klasse, das freut mich!

Gern geschehen :-)

---

Ich habe noch eine Aufgabe und bin mir nicht sicher ob ich die richtig machen kannst du mal drüber schauen?

Es wird zweimal geworfen. Mit welcher Wahrscheinlichkeit wirft man
a) zweimal eine 6
b) zuerst eine 6, dann eine 3
c)zuerst eine 6, dann eine andere Zahl
d) zwei verschiedene Zahlen, dabei eine 6 (als erste oder zweite)
e) zwei verschiedene Zahlen
f) zwei gleiche Zahlen

Antwort:
a) 6/36= 16,67%
b) 2/36= 5,5%
c) 2/36= 5,5%
d) 3/36= 8,3%

---

Da liegst Du leider völlig daneben :-(

Mach Dir nachfolgende Berechnungen auch mal an einem Baumdiagramm klar. Entlang des Pfades wird multipliziert, ganz am Schluss werden die Wahrscheinlichkeiten aller passenden Ergebnisse addiert.

Es wird zweimal geworfen. Mit welcher Wahrscheinlichkeit wirft man

a) zweimal eine 6

1/6 * 1/6 = 1/36 ≈ 0,0278 = 2,78%

b) zuerst eine 6, dann eine 3

1/6 * 1/6 ≈ 2,78%

c)zuerst eine 6, dann eine andere Zahl (also keine 6?)

1/6 * 5/6 = 5/36 ≈ 13,89%

d) zwei verschiedene Zahlen, dabei eine 6 (als erste oder zweite)

6x oder x6

1/6 * 5/6 = 5/36 ≈ 13,89%

5/6* 1/6 ≈ 13,89%

Gesuchte Wahrscheinlichkeit also

10/36 ≈ 27,78%

e) zwei verschiedene Zahlen

1 * 5/6 = 5/6 ≈ 83,33%

f) zwei gleiche Zahlen

1 * 1/6 = 1/6 ≈ 16,67%

Rückfragen sind gern gesehen :-)

Besten Gruß

---

bei der b da steht ja zuerst eine 6 und dann eine 3.

warum rechnet man 1/6 * 1/6? Weil es nur zwei zahlen sind?

---

Analog zu Deiner Aufgabe mit den Rhesusfaktoren hast Du ja jetzt auch zwei Abzweigungen (Rhesusfaktoren waren Frau + Mann, hier sind es 1. Wurf und 2. Wurf).

Bei den Rhesusfaktoren gab es aber jeweils nur 2 Äste, nämlich positiv und negativ; und damit 4 "Endergebnisse":

++, +-, -+, ++

Bei einem normalen Würfel hast Du aber jeweils 6 Äste, nämlich 1, 2, 3, 4, 5 und 6; und damit 36 "Endergebnisse":

11, 12, ... , 63, 64, 65, 66

Die Wahrscheinlichkeit, im ersten Wurf eine 6 zu würfeln beträgt 1/6; und die Wahrscheinlichkeit, danach im 2. Wurf eine 3 zu würfeln, beträgt ebenfalls 1/6. Diese Wahrscheinlichkeiten miteinander multipliziert ergibt

1/6 * 1/6 = 1/36. Und es gibt von den 36 "Endergebnissen" nur dieses eine, das passt!

---

Ahh okay ich dachte nämlich man müsste iwas mit 3/36 nehmen. aber wann muss man nicht mehr 1/6 nehmen sonder z.B. 3/36?

____________________________________

Ich habe hier noch eine gerechnet:

Es wird dreimal gewürfelt. mit welcher wahrscheinlichkeit wirft man dabei eine einzige 6.

1/6*1/6*1/6= 1/216= 4,6% ist das so richtig?

---

3/36 wäre zum Beispiel die Wahrscheinlichkeit, erst eine 6 und dann eine ungerade Zahl zu werfen:

P(6) = 1/6

P(ungerade) = 1/2 = 3/6

P(6 und dann ungerade) = 1/6 * 3/6 = 3/36

Es wird dreimal gewürfelt. mit welcher wahrscheinlichkeit wirft man dabei eine einzige 6.

1/6*1/6*1/6= 1/216= 4,6% ist das so richtig?
Falsch: Du hast berechnet, wie groß die Wahrscheinlichkeit ist, 3 mal hintereinander eine 6 zu werfen.
Richtig wäre:
P("genau eine 6") = P(6xx) + P(x6x) + P(xx6) = 3 * 1/6 * 5/6 * 5/6 = 75/216 ≈ 34,72%

---

du hast die 5/6 genommen weil die dann sozusagen "wegfällt" und in der 1/6 wiederspiegelt oder?

---

Ich habe die 5/6 genommen, weil das die Wahrscheinlichkeit ist, keine 6 zu würfeln. Die Wahrscheinlichkeit, eine

6 zu würfeln, ist dagegen 1/6. Diese beiden Wahrscheinlichkeiten addieren sich zu 5/6 + 1/6 = 6/6 = 1 = 100%, das ist die W. für das "sichere" Ereignis, welches in jedem Fall eintritt: Entweder man würfelt in einem Wurf eine 6 oder aber keine 6 - was anderes ist nicht möglich!

Angenommen, wir werfen zuerst eine 6 und dann keine 6 und schließlich nochmals keine 6. Wie groß ist die Wahrscheinlichkeit dafür? W. für eine 6: 1/6. Dann W. für keine 6: 5/6. Dann W. für keine 6: 5/6. Also ist

P(6xx) = 1/6 * 5/6 * 5/6 = 25/216

Immer an das Baumdiagramm denken!

Die 6 kann aber auch stattdessen beim 2. oder 3. Wurf geworfen werden (x|6|x bzw. x|x|6), deshalb ist die Gesamtwahrscheinlichkeit 3 * 25/216 = 75/216.