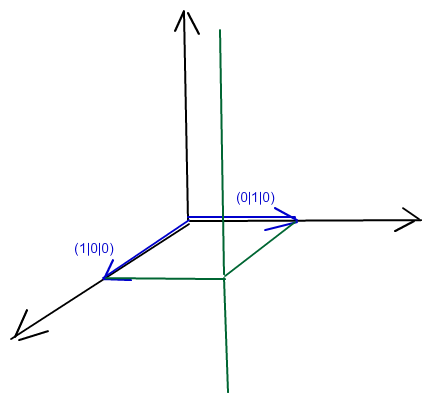
Die gesuchten Vektoren liegen in der vertikalen Ebene, die durch die z-Achse und die grüne Gerade aufgespannt wird.
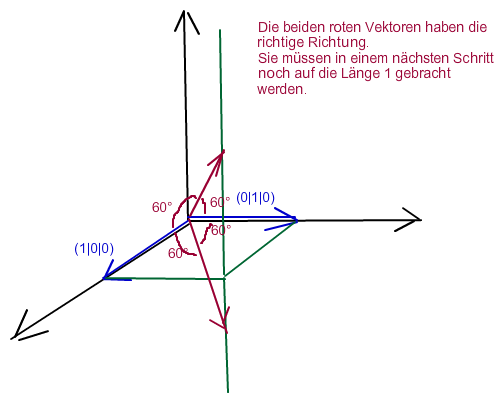
Berechnen kannst du die Richtung der roten Vektoren, wie in der andern Antwort erklärt, mit dem Skalarprodukt.
Ansatz: v = (a|a|b)
Wobei (a|a|b) * (1|0|0) = cos(60°) * √(2a^2 + b^2) * 1
a = 1/2 * √(2a^2 + b^2)
Weil die Länge √(2a^2 + b^2) = 1 vorgegeben ist, folgt
a = 1/2
einsetzen in
√(2a^2 + b^2) = 1
√(1/2 + b^2) = 1
b^2 = 1/2
b = ±√(1/2)
v1 = ( 1/2 | 1/2 | 1/√2)
v2 = (1/2 | 1/2 | -1/√2)