Inverse berechnen und beide Funktionsgraphen zeichnen

Question

Hallo ich stecke gerade bei einem Beispiel fest

Und zwar habe ich folgende Funktion:

f(x)=sqrt(3+1/2x) mit der inversen y=2(y^2-3). Ich habe dann die inverse gezeichnet, was ja eine parabel ist und wollte daraus dann die hauptfunktion zeichnen. Aber nach ein bisschen rumgrübeln ist mir dann eingefallen, dass die inverse ja injektiv ist da man für verschiedene x-werte ja den gleichen Funktionswert heraus bekommt und dadurch die funktion ja keine inverse hat. Liege ich da soweit richtig? Wenn ja, gilt das Beispiel somit als gelöst indem ich nur die inverse berechne und diese dann gezeichnet habe?

Answer 1

zu deiner Frage: deine Funktion ist bijektiv bezüglich ihres Definitions- und Wertebereiches. Demnach invertierbar. Der Definitionsbereich der inversen Funktion ist der Wertebereich der ursprünglichen Funktion. Demnach brauchst du die Funktion auch nur dort einzuzeichnen.

Gruß

Comments

Das heißt ich müsste die Hauptfunktion theoretisch für die Werte [-6,+∞] zeichnen.

---

Jo obwohl ich bezweifele, dass du bis unendlich zeichnen musst :D wichtig ist hierbei, dass die Funktion für x<-6 nicht definiert ist (jedenfalls über den reellen Zahlen).

---

Das hatte ich jetzt auch nicht vor :) Danke nochmals.

---

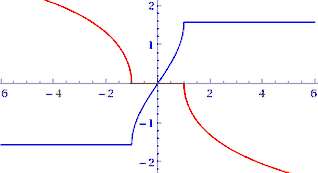
Für reelle Zahlen alles klar.

Frage: man kann ja Wurzelfunktionen auch mit komplexen Anteil zeichnen. Im Bild die rote Kurve für x kleiner  -6.

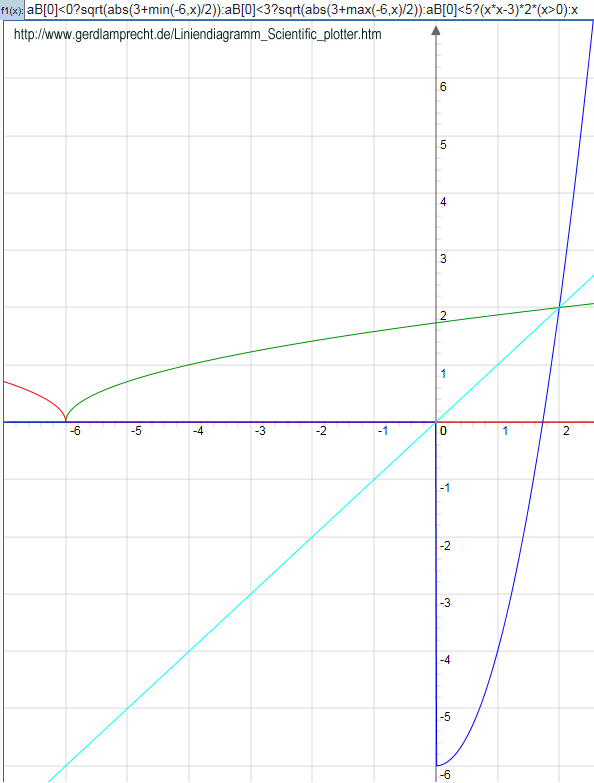
  Wie sieht es nun für die inverse Funktion aus?  

Technisch gesehen könnte ich einen weiteren ELSE-Zweig einbauen (weitere Farbe) und die blaue Kurve bei y=-6 (nach unten) spiegeln, so dass die türkise Spiegelgrenze f(x)=x für x und y kleiner -6 wäre...  

ABER dann ist die INVERSE im Sinne der "Eindeutigkeit einer Funktion" nicht mehr Eindeutig...

Was sagen Lehrer/Mathematiker, wenn auch der komplexe Zweig mit gezeichnet werden soll?  

Oder ist es wie bei der asin(x) -> da gibt es ja auch 2 mögliche Bilder:

a) einfach die sin-Kurve um 90° gedreht  

b) mit komplexen Anteil (rot): 

 

---

Ich glaube es funktioniert nur mit der Invertierung, wenn man beide Anteile getrennt betrachtet:  

a) f(x) = Re((sqrt(3-x/2)) -> mit ihrer Inversen

b) f2(x) = Im(...) -> mit ihrer Inversen

Answer 2

f ( x ) = √ (3+1/2 * x )

Def-Bereich [ -6 ; ∞]
Wertebereich [ 0 ; ∞ ]

inverse Funktion
g ( x ) = 2 * ( y² - 3 )

Def-Bereich [ 0 ; ∞ ]
Wertebereich [ -6 ; ∞]

 

Zum manuellen Zeichnen brauchst du nur einige Wertepaare
auszurechen ( -6  | 0 ).
Zum Zeichnen der inversen Funktion vertauschst du die x und y Koordinaten
( 0 | -6 ).
Oder du spiegelst die Funktion an der Winkelhalbierenden des 1.Quadranten.

mfg Georg