Welche Jahresförderung plant die Energiepolitik in Zukunft? Wie viel Kohle wird 2030 gefördert?

Question

Aufgabe:

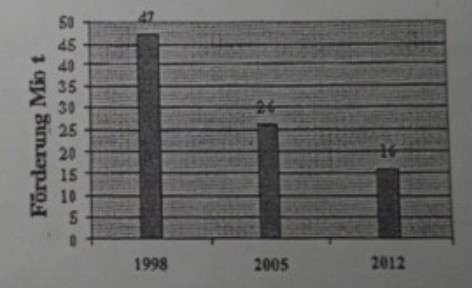
Das Diagramm zeigt die Förderung von Steinkohle im Jahr 1998 und die politischen Vereinbarungen bis 2012.

a) Bestimmen Sie ein Modell unter der Annahme, dass die Förderung einer Funktion f mit \( f(t)=a+b e^{-k t} \) genügt (1998: t=0).

(Lösung: \( f(t)=6,91+40,09 e^{-0,106 t} \) )

Welche Jahresförderung plant die Energiepolitik in der Zukunft?

b) Bestimmen Sie dann die Gesamtförderung bis 2030. Wie viel Kohle wird im Jahr 2030 gefördert?

c) Wie hoch ist die durchschnittliche Jahresförderung uber den Zeitraum 1998 - 2030 ?

Ansatz/Problem:

Ich hab sie soweit, dass ich aus dem Schaubild folgende drei Gleichungen entnommen habe:

1. f(0) = 47 also a+b= 47
2. f (7) = 26 also a+be^{-7k} =26
3. f(14)=16 also a+be^{-14k} = 16

Answer 1

2030  -------> = 6,91+ 40,09  *  e ^-0,106  * 32 =  6,91 + 1,33 = 8,24 Mio t !!

Comments

danke aber ich muss ja erstmal auf die Gleichung kommen und weiß nicht wie. Die Lösung steht ja schon in der AUfgabe aber ich will selber drauf kommen..