Aufgabe:
Das Schwimmbad in Wuppertal ist wegen der parabelförmigen Dachlinie und der vielen Glasflächen über Wuppertal hinaus bekannt. Um die Größe der abgebildeten Glasfläche abzuschätzen (vgl. Foto), wird die gesamte Glasfläche in zwei Teilflächen zerlegt: Der untere Teil ist ein symmetrisches Trapez, darüber ist die Fläche durch die parabelförmige Dachlinie begrenzt (siehe Abbildung).
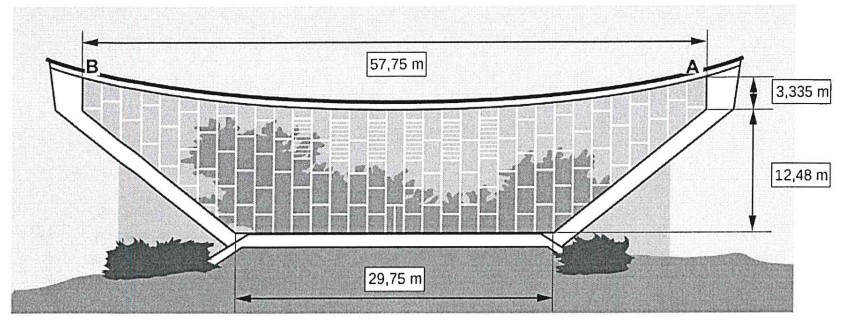
a) Zeigen Sie, dass der Flächeninhalt der trapezförmigen Glasfläche \( 546 \mathrm{~m}^{2} \) beträgt.
Die obere Kante der Glasfläche kann durch eine Parabel mit der Funktionsgleichung \( f(x)=0,004 x^{2} \) angenähert beschrieben werden. In Abbildung 2 wurde der Funktionsgraph mit Hilfe einer Geometriesoftware in ein geeignetes Koordinatensystem gezeichnet.
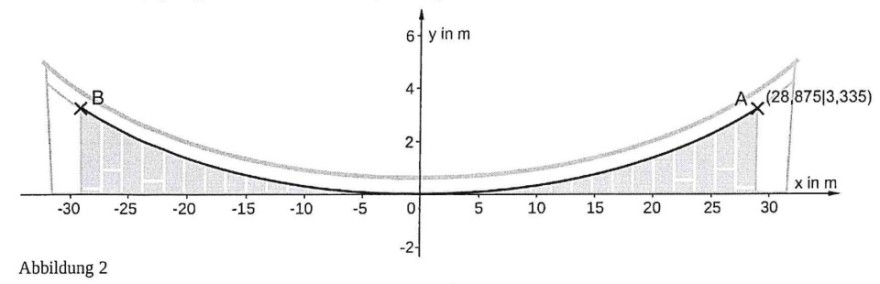
b) Weisen Sie rechnerisch nach, dass der Punkt \( A(28,875 \mid 3,335) \) annähernd auf der Parabel \( f \) liegt.
c) Geben Sie die Koordinaten des Punktes \( B \) an. Begründen Sie die Werte der Koordinaten für den Punkt \( B \) mit Hilfe der Parabeleigenschaften.