Besser, wenn Du Dich bei Arrays (Feldvariablen) wie bei fast allen Programmiersprachen schon mal an eckige Klammern gewöhnst, da man es dann nicht mit Multiplikation eines normalen Klammerausdrucks verwechselt:
y[t] := y[t-1] + y[t-2]
in Worten: Feldvariable y[ ] mit Index t ergibt sich aus Vorgänger (mit Index [t-1] ) + Restfunktion
Restfunktion y[t-2] ist aber eine von t abhängige Funktion (Vor-Vorgänger) und keine konstante Zahl a!
y[5] = y[5-1] + y[5-2] = y[4] + y[3] = 5 + 3 = 8
denn y[3] = y[2] + y[1] = 2 + 1
und das ist kein lineares Wachstum, wie man an der expliziten Formel sehen kann:
Iterationsrechner http://www.gerdlamprecht.de/Roemisch_JAVA.htm#ZZZZZ0008 Beispiel 8 leicht angepasst
zeigt alle 3 Algorithmen:
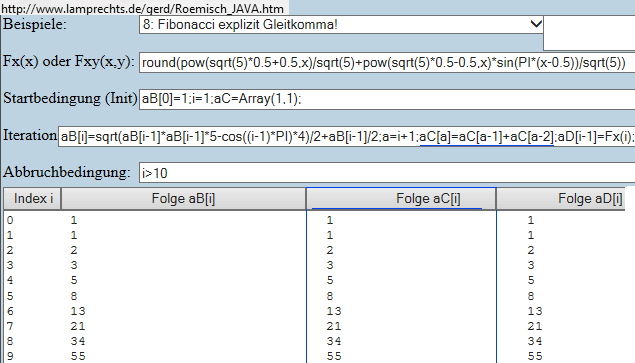
aC[i] ist Dein y[t] -> rekursive Form aus 2 Vorgängern
aB[i] ist rekursiv, jedoch aus nur 1 Vorgänger berechnet
aC[i] ist rein explizit, d.h. man kann beliebige reelle & komplexe Zahlen einsetzen (ohne Vorgänger)
(vergl. http://www.lamprechts.de/gerd/php/RechnerMitUmkehrfunktion.php Fibonacci(x) )
Hinweis: Wissenschaftler haben Fibonacci(0) =0 definiert
d.h. bei Index 1 und 2 gibt's das Ergebnis 1 -> also gegenüber Deiner Aufgabenstellung nur eine Offset-X um 1 verschobene Funktion:
Fibonacci(x) = y[x-1] weil nur die beiden Startwerte anders:
Fibonacci(1)=y[0]=1
Fibonacci(2)=y[1] =1
Andere Startwerte (wie 1 und 3) ist bekannt als Lucas-Funktion.