Zeigen Sie, dass die Gerade die Fläche in zwei Teilflächen gleichen Inhalts teilt.

Question

Aufgabe:

Gegeben ist die Funktion \( f \) mit \( f(x)=-6 x^{2}+12 x+18, x \in \mathbb{R} \). Die Abbildung zeigt den Graphen von \( f \), der durch die Punkte \( H(1 / 24) \) und \( N(3,0) \) verläuft.

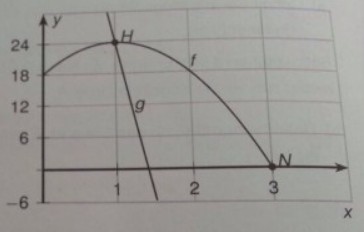
a) Zeigen Sie, dass \( \int \limits_{0}^{1} f(x) d x=22 \) gilt.

b) Die Fläche, die der Graph von \( f \) im ersten Quadranten mit den Koordinatenachsen einschließt, hat den Inhalt \( 54 \). Eine Gerade \( g \) verläuft durch den Punkt \( H \) und hat die Steigung \( m=-57,6 \).

Zeigen Sie, dass die Gerade \( g \) die Fläche, die der Graph von \( f \) im ersten Quadranten mit den Koordinatenachsen einschließt, in zwei Teilflächen gleichen Inhalts teilt.

Ansatz/Problem:

Wie rechnet man Aufgabe b aus, was muss man da machen? Ich habe keinen Taschenrechner.

Comments

Das mit dem Taschenrechner kann dir keiner abnehmen. Organisiere ein Modell, das du schon öfters mal bedient hast, vor Ort.

Üben kannst du auch damit: https://www.wolframalpha.com/ 

Answer 1

b ) Berechne z. B. die linke Hälfte der Fläche F wie folgt.

F = F1 + F2

Wobei

F1 = ∫_(0)^1 f(x) dx

F2 = 24 * (x_(1) - 1 ) / 2

x_(1) ist die Nullstelle der eingezeichneten Geraden durch H. Deren Gleichung bestimmst du zuerst. Anleitung dazu:

Wenn F1 + F2 = 27 , hast du das Verlangte gezeigt.