Aufgabe:
\( \vec{D}=\frac{1}{4 \pi} \int \limits_{\mathrm{Weg}} \frac{\lambda \mathrm{d} z^{\prime}}{a^{2}} \vec{e}_{a}=\frac{1}{4 \pi} \int \limits_{\mathrm{Weg}} \frac{\lambda \mathrm{d} z^{\prime}}{a^{3}} \vec{a} \)
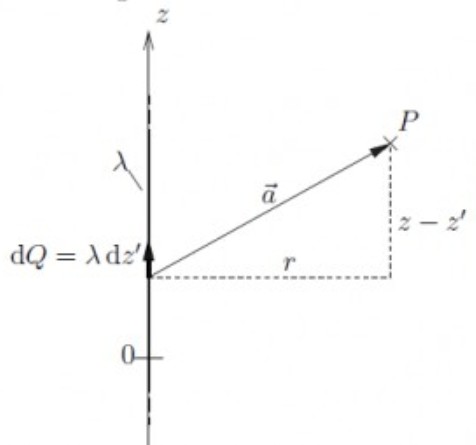
Für einen Punkt \( P=(r, 0, z) \) in Zylinderkoordinaten ergibt sich unter zulässiger Vernachlässigung der Winkelposition (rein radiales Feld) der folgende positionsabhängige Abstandsvektor:
\( \vec{a}=\left(\begin{array}{c}r \\ 0 \\ z-z^{\prime}\end{array}\right) \), mit \( a=\sqrt{r^{2}+\left(z-z^{\prime}\right)^{2}} \)
Ansatz/Problem:
Ich weiss nicht, wie der Vektor a herausgefunden wurde. Das Koordinatensystem ist ein Zylinderkoordinatensystem, das heisst dreidimensional x y z.