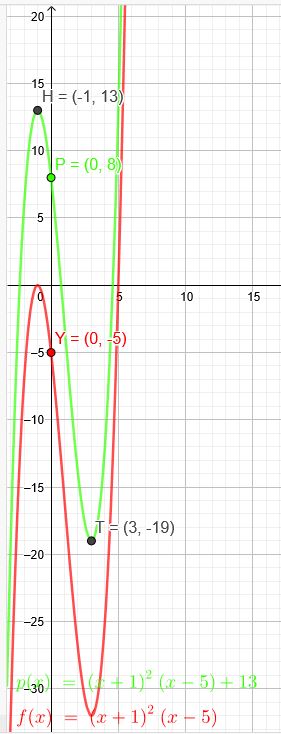
Der Graph einer Polynomfunktion vom Grad 3 hat eine lokale Extremstelle bei \(x=3\) und eine weiter lokale Extremstelle bei \(x= -1\) Im Schnittpunkt P\((0|8)\) mit der 2. Achse ist die Steigung der Tangente \(m=-9\).
\(f(x)=a[(x+1)^2(x-N)]\)
lokale Extremstelle bei \(x= -1\):
\(f'(x)=a[2(x+1)(x-N)+(x+1)^2]\)
lokale Extremstelle bei \(x=3\):
\(f'(3)=a[2\cdot(3+1)(3-N)+(3+1)^2]=a(40-8N)=0\)
\(N=5\):
\(f'(x)=a[2\cdot (x+1)(x-5)+(x+1)^2]\)
P\((0|...)\) Steigung der Tangente \(m=-9\):
\(f'(0)=a[2\cdot (0+1)(0-5)+(0+1)^2]=-9a=-9\)
\(a=1\):
\(f(x)=(x+1)^2(x-5)]\)
\(f(0)=(0+1)^2(0-5)=-5\):
Hier ist nun der Schnittpunkt mit der 2. Achse Y\(0|-\red{5})\).
Er soll aber bei P\((0|\red{8})\) liegen:
\(p(x)=(x+1)^2(x-5)+\red{5}+\red{8}=(x+1)^2(x-5)+13\)