Erkennen ob das Dreieck spitzwinklig, stumpfwinklig usw. ist? Kongruenzsätze

Question

Wie erkenne ich denn ob ich ein dreieck eindeutig konstruieren kann ohne es zu zeichnen? also wenn da steht beispielsweise: (Beta)= 78° a=5cm c=9 cm?

 

Und wie erkenne ich ob ein Dreieck spitzwinklig, stumpfwinklig oder gleichschenklig ist??

 

Wie lauten die Kongruenzsätze?  also sss oder sws oder so

und wie erkenne ich sie?

Comments

Die Kongruenzsätze lauten sss sws, wsw sws Ssw Das geht nur über die Winkelsumme im Dreieck

Answer 1

Hi

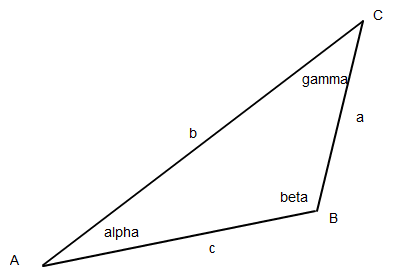
Ich denke es hilft, wenn man das allgemeine Dreieck und die dazugehörige Beschriftung auswendig kann (Eckpunkte gegen den Uhrzeigersinn, in alphabetischer Reihenfolge, bei A beginnend antragen; Seiten gegenüber den Eckpunkten usw.). Eindeutig konstruieren lässt sich ein Dreieck, wenn einer der vier Kongruenzsätze zutrifft.
In deinem Fall (beta= 78° a=5cm c=9 cm) bedeutet das sws.

Man erkennt um welchen Satz es sich handelt, wenn man weiß wie die Winkel und Seiten im Dreieck liegen (um sicher zu sein, musst Du im konkreten Anwendungsfall herausfinden wie die Anordnung ist, es muss nicht immer so sein wie ich es oben gezeichnet habe, meistens kann man jedoch davon ausgehen). In Deinem Fall schaust Du am besten auf die Skizze, falls Du keine hast machst Du Dir am besten eine; das ist sicherer als das im Kopf auszuknobeln. Du siehst: c, beta, a also Seiten mit eingeschlossenem Winkel = sws ist also eindeutig konstruierbar. (Siehe auch [1]).

Zwei Dreiecke sind kongruent, wenn sie übereinstimmen in:
(1) drei Seiten
      (sss) --> Kosinussatz für fehlende Winkel/Seiten
      Bsp.: a,b,c
(2) zwei Seiten und dem eingeschlossenen Winkel:
      (sws) --> Kosinussatz für fehlende Winkel/Seiten
      Bsp.: b,alpha,c
(3) einer Seite und zwei Winkeln:
      (wsw) oder (sww) --> Sinussatz für fehlende Winkel/Seiten
      Bsp.: alpha,c,beta oder c,beta,gamma
(4) zwei Seiten und dem Gegenwinkel der größeren Seite:
      (Ssw) --> Sinussatz für fehlende Winkel/Seite
      Bsp.: b,c,beta

Zu (4): Wenn der Winkel gegenüber der kleineren Seite liegt, dann kann es passieren, dass es zwei Lösungen gibt.

 

Spitzwinkliges Dreieck: Alle Winkel sind kleiner als 90°. [2]
Stumpfwinkliges Dreieck: Es gibt einen Winkel der größer als 90° ist. [3]
Gleichschenkliges Dreieck: Zwei Winkel sind gleich und zwei Seiten sind gleich. (Wenn zwei Winkel gleich sind, dann sind auch zwei Seiten gleich und umgekehrt.) [4]

[1] https://de.wikipedia.org/wiki/Kongruenzsatz
[2] https://de.wikipedia.org/wiki/Spitzwinkliges_Dreieck
[3] https://de.wikipedia.org/wiki/Stumpfwinkliges_Dreieck
[4] https://de.wikipedia.org/wiki/Gleichschenkliges_Dreieck

 

lg JR