Von Normalform in Scheitelpunktform f(x)= -1/3 x² -2/3x +5/3 ---> f(x)= -1/3 (x²+2x-5) dieser Schritt?

Question

Von Normalform in Scheitelpunktform
f(x)= -1/3 x² -2/3x +5/3

f(x)= -1/3 (x²+2x-5)        <-- Wie komme ich da Drauf ?????

f(x)= -1/3 (x²+2x + (1)² - (1)² -5) <-- Quadratische Ergänzung

f(x)= [(x+1)² -6)]

Scheitelpunktform f(x)= -1/3 (x+1)+2

Bitte ganz simple erklärungen sonst raff ich das nicht :/

Answer 1

Hi Maike

Gleichung:
f(x)= -1/3 x² -2/3x +5/3

1. Ausklammern:

f(x)= -1/3 (x²+2x-5)        <-- Wie komme ich da Drauf ?????

Man klammert -1/3 aus. Das sieht dann folgendermaßen aus (ich schreibe den Faktor -1/3 in Klammern um ihn noch etwas besser optisch abzugrenzen):
f(x)= -1/3 x² -2/3x +5/3 = (-1/3) * x² + (-1/3) * 2*x + (-1/3) *(-5);

(-1/3) kann man nun ausklammern:
f(x) = (-1/3) * [x² +2*x -5];


2. Quadratische Ergänzung:

f(x)= -1/3 (x²+2x + (1)² - (1)² -5) <-- Quadratische Ergänzung

Beim quadratischen Ergänzen nimmt man sich die 1. binomische Formel zum Vorbild:
a^2 +2*a*b +b^2  =  (a +b)^2;

Nun schauen wir uns den gelben Teil deiner Funktion an f(x) = (-1/3) * [x² +2*x -5] und vergleichen ihn mit der binomischen Formel, dazu schreibe ich mal beide untereinander:
a² +2*a*b +b²
x² + 2*x      -5
a² = x² passt schon mal ganz gut
2*a*b = 2*x scheint noch nicht so ganz zu passen vor allem da ja b²=5 zu sein scheint
nun schreiben wir 2*x noch etwas anders: 2*x*1 mit 1 multiplizieren ist erlaubt und ändert nichts an dem Term
Vergleichen wir nochmal:
2*a*b
2*x*1
Sagen wir also b = 1

Damit das zur binomischen Formel passt müsste da noch das passende b = 1 stehen, also:
a² +2*a*b +b²
x² + 2*x*1  +1^2 -1^2     -5
Damit die Gleichung wieder stimmt muss man noch -1 abziehen. Man addiert also 1 und zieht gleich wieder 1 ab. Damit ändert sich der Term insgesamt nicht, man kann ihn aber anders zusammenfassen:
a² +2*a*b +b²
(x² + 2*x*1  +1²)   -(1^2     +5)

Nun kannst Du leicht erkennen, dass der Teil der binomischen Formel entspricht und die kann man auch anders schreiben:
(a +b)²;
(x + 1)²   -6;

 

3. Ausmultipliziern, vollständige Funktion in Scheitelpunktform:

f(x) = (-1/3) * [ (x + 1)²   -6 ]  =  -1/3 * (x + 1)²   +2;

 

4. Erklärung zur Scheitelpunktform:

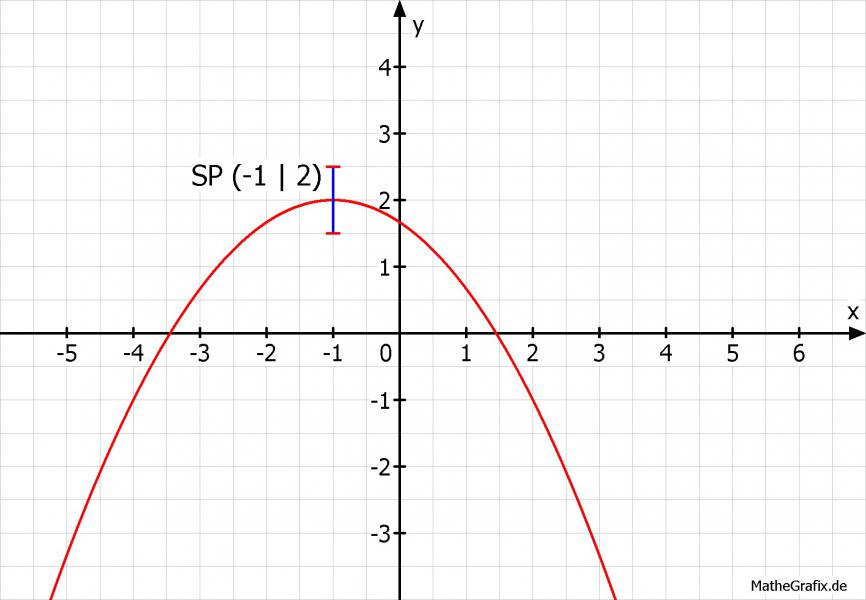
Bei der Scheitelpunktform kann man den Scheitelpunkt der Parabel leicht ablesen.
Hier liegt der Scheitelpunkt bei SP(-1 | 2). Um das leicht ablesen zu können schreibt man die Gleichung am besten so:   f(x) =    -1/3  (x -  (-1) )   +2 . Der Scheitelpunkt ist also um 1 nach links und um 2 nach oben verschoben.
 

 

Ich hoffe es ist nachvollziehbar.

lg JR

Comments

Hab doch nochmal eine Frage 

wie kommst du von der herkömmlichen Funktion zu dieser hier --> f(x)= -1/3 (x²+2x-5) ?

wo kommt da plötzlich die 2x-5 her ? Wie rechne ich das ?

---

Bei der Funktion f(x)= -1/3 x² -2/3x +5/3 kann man bei jedem der Summanden -1/3 ausklammern, also:
#   -1/3 x² = (-1/3) * x²;
#   -2/3x   = -2  *  1/3  * x = (-1/3) *2*x;
#   5/3      = 5 * 1/3 = (-1) * (-1) * 5 * 1/3 = (-1/3) * (-5);

Ich habe die einzelnen Teile der Funktion mittels Äquivalenzumformung umgeformt. Die Funktion sieht nun nach der Umformung so aus:
f(x) = (-1/3) * x²  + (-1/3) *2*x + (-1/3) * (-5);

Mit dem Distributivgesetz gilt, das heißt erstmal allgemein a*b  +a*c  +a*d  =  a* (b +c +d) .
Verglichen mit der Funktion:
           a  * b   +      a    * c   +     a     *d
f(x) = (-1/3) * x²  + (-1/3) *2*x + (-1/3) * (-5)

(-1/3) kann man so wie a einfach ausklammern
          a    * [b   + c     + d     ]
f(x) = (-1/3) * [ x²  + 2*x + (-5) ]

 

Hoffe das hilft. Falls nicht --> Kommentar.

lg JR