Hi
1. Skizze:
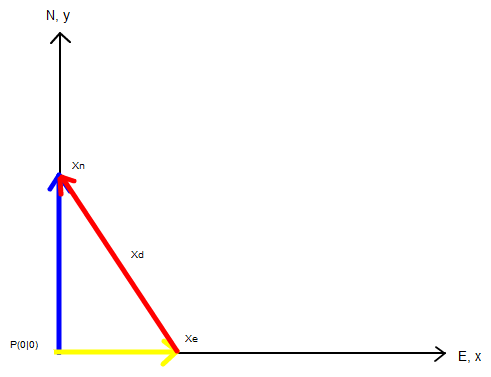
2. Angaben:
vEx = 32 kn;
vNy= 24 kn;
Zuordnung: Uhrzeit - Zeitpunkt| Uhrzeit | 08.00 | 09.00 | 10.00 | 11.00 |
| Zeitpunkt tn | t0= 0h | t1= 1h | t2= 2h | t3= 3h |
3. Ansatz:
Ich werde die Einheiten Knoten (kn), Seemeile (sm) und Stunde (h) verwenden. (1 kn = 1 sm/h; 1 sm = 1,852 km)
Ich beschreibe zunächst die Position der Schiffe mit Hilfe von Vektoren:
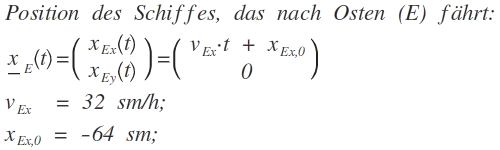
xEx,0 = -64 sm; // ergibt sich da das Schiff zum Zeitpunkt t2 = 2 h bei P(0|0) ankommt.
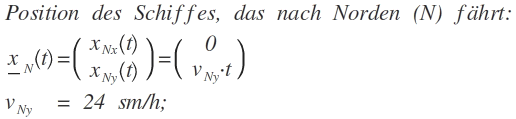
4. Rechnung:
Damit ergibt sich für die Distanz zwischen den Schiffen und die zeitliche Änderung der Distanz ( = die erste Ableitung der Distanz nach der Zeit):

Nun musst Du nur noch die entsprechenden Werte einsetzen und die Ergebnisse für t1 und t3 berechnen.
5. Ergebnisse:
Ich schreib Dir noch die Ergebnisse auf, die ich berechnet habe.
d_punkt(t = 1h) ≈ -11,2 sm/h;
d_punkt(t = 3h) ≈ +34,9 sm/h;
6. Abschließende Bemerkung:
Bitte alles kritisch prüfen. Ich kann Dir keine Garantie darauf geben, dass alles richtig ist. Falls Du Fragen hast --> Kommentar.
lg JR