Wie bestimme ich den Abstand einer Hyperbel und Geraden?

Question

:)

Ich soll den Abstand d einer Hyperbel 

$$H:=\left\{ \left( x,y \right) \in ℝ^{ 2 }|{ x }^{ 2 }-{ y }^{ 2 }=1 \right\}$$

zu einer Geraden 

$$G:=\left\{ \left( u,v \right) \in  ℝ^{ 2 }| v=2u \right\}$$

bestimmen.

Der Abstand ist hierbei definiert durch $$d:=inf\left\{ { \left\| h-g \right\|  }_{ 2 } |h\in H,g\in G \right\}$$

Ich habe nur eine kleine Idee, wie die Aufgabe funktionieren könnte, aber bin mir dennoch sehr unsicher. Und zwar vermute ich, dass wir den kleinsten Abstand von h und g bestimmen sollen, da es sich ja um das Infimum handelt. Nach der Definition des Abstandes müsste ich eigentlich zuerst die Funktionen h ung g voneinander subtrahieren, also die Differenz nehmen, und darauf die 2-Norm anwenden. Aber wie stelle ich g und h auf? Ich kann die Funktionen ja nicht einfach nach y bzw. u auflösen und diese dann einfach mit g und h bezeichnen.

Ich wäre für eine Hilfe sehr dankbar :) 

Gruß

Answer 1

h: y = √(x^2 - 1) [und ebenso eine im Negativen Bereich. Die interessiert mich aber nicht.]

g: y = 2·x

h': y = x/√(x^2 - 1) = 2 --> x = 2/3·√3

y = √((2/3·√3)^2 - 1) = 1/3·√3 --> [2/3·√3 ; 1/3·√3]

l: y = - 1/2·(x - 2/3·√3) + 1/3·√3 = 2·√3/3 - x/2

Schnittpunkt l und g

2·√3/3 - x/2 = 2·x --> x = 4/15·√3

y = 2·4/15·√3 = 8/15·√3 --> [4/15·√3 ; 8/15·√3]

d = |[2/3·√3 ; 1/3·√3] - [4/15·√3 ; 8/15·√3]| = √15/5 = 0.7746

Skizze:

Comments

Dankeschön :D

Also hab das soweit verstanden und auch nochmal selbst nachgerechnet, aber drei Schritte verstehe ich nicht so ganz:

(1) h': y = x/√(x² - 1) = 2 --> x = 2/3·√3

Was wird hier gemacht? Also klar ist ja, dass man h ableitet. Aber wo kommt die 2 nach dem Gleichheitsszeichen her? Hat man g auch abgeleitet und dann h' = g' gesetzt und dann das x berechnet?

(2) l: y = - 1/2·(x - 2/3·√3) + 1/3·√3

Wie kommt man auf diese Umformung?

(3) Schnittpunkt l und g

Warum sucht man den Schnitt von l und g? Hat man in den Schritten zuvor die Gerade soweit nach unten verschoben, dass man nun durch den Schnitt von Gerade und Hyperbel den zweiten Punkt, also den roten Punkt auf der Hyperbel, berechnen kann?

Danke in Voraus :D

---

Was wird hier gemacht? Also klar ist ja, dass man h ableitet. Aber wo kommt die 2 nach dem Gleichheitsszeichen her? Hat man g auch abgeleitet und dann h' = g' gesetzt und dann das x berechnet?

Ja 2 ist die Steigung von g. Du siehst an der Skizze das die Punkte die den kleinsten Abstand haben beide die Steigung 2 haben. Dann wird nur wie du sagst x berechnet.

Wie kommt man auf diese Umformung?

Das ist die Punkt-Steigungs-Form der Lotgeraden. Die Lotgerade ist Senkrecht zur Steigung 2 und hat damit die Steigung -1/2. Weiterhin geht sie durch den ermittelten Punkt.

Warum sucht man den Schnitt von l und g? Hat man in den Schritten zuvor die Gerade soweit nach unten verschoben, dass man nun durch den Schnitt von Gerade und Hyperbel den zweiten Punkt, also den roten Punkt auf der Hyperbel, berechnen kann?

Genau. Durch die Punkt-Steigungs-Form befindet sich die Lotgerade genau dort wo ich sie haben will. 

---

Achso Okay vielen Dank :D
Jetzt habe ich alles verstanden

Das mit der Punkt-Steigungs-Form der Lotgeraden, da habe ich gar nicht mehr dran gedacht.

Danke für Alles :D

---

Ich habe nochmal eine Frage:

Weiß vielleicht jemand, wieso die Funktion gerade dort optimiert wurde, wo die Steigung der beiden Graphen gleich ist?

---

... wieso die Funktion gerade dort optimiert wurde, wo die Steigung der beiden Graphen gleich ist?

drehe doch das Bild oben in der Antwort so hin, dass die Gerade \(v=2u\) horizontal liegt:

was siehst Du?

---

Hallo,
vielleicht so : wenn ich eine beliebige Normale zu " v " einzeichne  und diese parallel verschiebe
treffe ich auf einen Punkt auf der Hyperbel
welcher den kürzesten Abstand hat.
Zeichne ich nun eine Normale auf der Normalen
im Punkt ein ist die Steigung gleich der
Steigung der Geraden.
mfg Georg

Answer 2

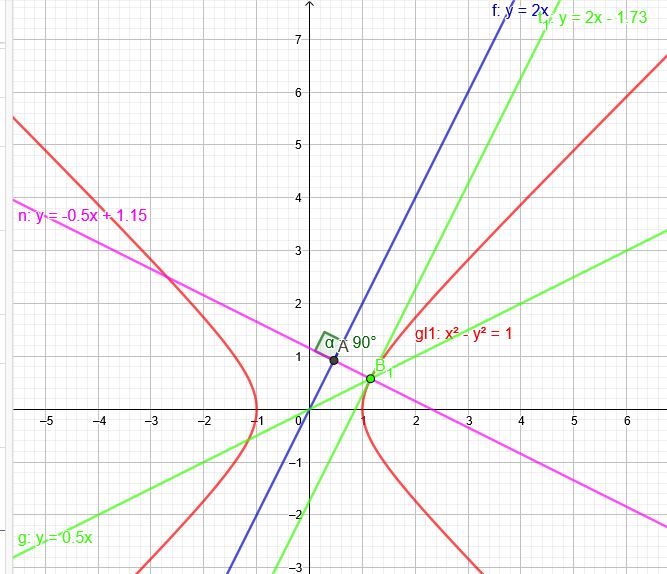
\(H:=\left\{ \left( x,y \right) \in ℝ^{ 2 }|{ x }^{ 2 }-{ y }^{ 2 }=1 \right\}\)  parallel zu   \(y=\red{2}x\)    → \(m=\red{2}\)

Eine Parallele zu \(y=\red{2}x\) berührt die   Hyperbel in B.

\(f(x,y)=x^2-y^2-1\)

\(f_x(x,y)=2x\)

\(f_y(x,y)=-2y\)

\(f'(x)=-\frac{2x}{-2y}=\frac{x}{y}\)

\(\red{2}=\frac{x}{y}\)

\(y=0,5x\)  Schnitt mit der Hyperbel führt zum Berührpunkt:

\(x^2-0,25x^2=1\)        \(\frac{3}{4}x^2=1\)     \(x_1=\frac{2}{3}\sqrt{3}\)

\(\frac{4}{3}-y^2=1\)        \(y_1=\frac{1}{3}\sqrt{3}\)  →\(B_1(\frac{2}{3}\sqrt{3}|\frac{1}{3}\sqrt{3})\)

\(B_2\) bleibt außer Betracht.

Die Normale der Tangente in \(B_1\) \(n(x)=-0,5x+1,15\) schneidet die Gerade \( y=2x\) in A. Das ist nun der Punkt mit minimalstem Abstand zur Hyperbel. Nun noch den  Abstand ausrechnen.