Geoknecht - Das Online-Programm für Geometrie in 3D

Question

Nach dem Geozeichner 2D gehen wir eine Dimension weiter.

Hier ist die erste Version von "Geoknecht" - ein extrem hilfreiches 3D-Zeichenprogramm:

Link: https://www.matheretter.de/geoservant/de

Ihr könnt damit viele Stereometrie-Aufgaben und Problemstellungen, die Vektoren, Quader, Würfel, Kugeln, Polygone, Strecken und Dreiecke im Raum beinhalten, visualisieren und beantworten ;)

Die Navigation im 3D-Rendering erfolgt mit der Maus, linke Maustaste gedrückt halten, Maus bewegen, damit rotiert man die Kamera. Rechte Maustaste gedrückt halten, Maus bewegen, damit verschiebt man die Kamera im Raum. 

Alle 3D-Objekte werden per Text eingegeben, die Syntax ist sehr einfach:

Update 27 Feb 2017: Endlich habe ich es geschafft, ein Tutorial-Video (Einführung und Features) anzufertigen:

https://www.youtube.com/watch?v=OupOoi_lRw4

News-Meldungen zum Geoknecht:

https://www.mathelounge.de/tag/geoknecht

Anregungen und Ideen bitte als Kommentar.

Comments

Ich habe den Geoknecht weiterentwickelt, nun werden Vektoren und Vektorenlängen ausgerechnet, Streckenlängen, alle wichtigen Daten des Würfels (wie Flächendiagonale, Raumdiagonale, Flächen, Volumen), Daten des Quaders, Daten der Kugel, Flächeninhalt des Dreiecks im Raum (via Kreuzprodukt).

So lassen sich extrem schnell Objekte erstellen und deren Daten ablesen.

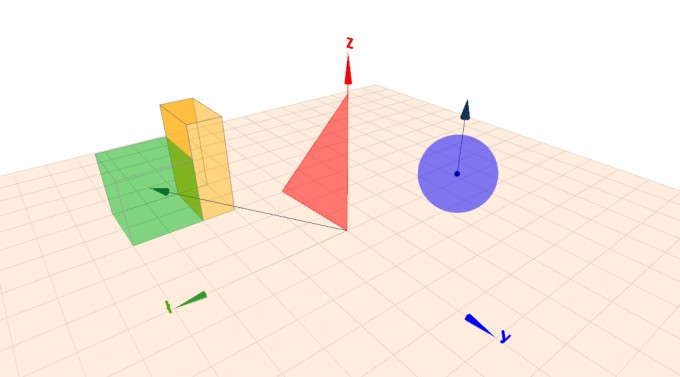
Link zum Beispiel

Mit folgenden Ergebnissen:

Kugel: r = 1 u = 6,283 A_K = 3,142 A_O = 12,566 V = 4,189
Vektor: v = (0|0|2) |v| = 2
Dreieck: a = 2,828; b = 2,828; c = 4 v_a = (0|0|4); v_b = (2|0|2); v_c = (-2|0|2); A = 8
Vektor: v = (4|-4|1) |v| = 5,745
Würfel: a = 2 d = 2,828 e = 3,464 u = 8 A_G = 4 A_M = 16 A_O = 24 V = 8 l = 24
Quader: b = 1; l = 2; h = 3 e = 3,742 u = 6 A_G = 2 A_M = 18 A_O = 22 V = 6 l = 24

Meine Fragen: 

1. Welche geometrische Körper möchtet ihr noch?

2. Was soll beim Polygon angezeigt werden? (Reichen die Streckenlängen und die einzelnen Vektoren?)

Schöne Grüße
Kai

---

1. Welche geometrische Körper möchtet ihr noch? 

Kannst du mit geoknecht die folgende Aufgabe illustrieren?

https://www.mathelounge.de/259458/gegeben-seien-die-beiden-punktmengen

Ebene und Gerade sowie Schnittmenge (Punkt) darstellen.

Punkt am besten mit dem zugehörigen Koordinatenquader.

---

Punkte lassen sich einzeichnen, Geraden habe ich soeben hinzugefügt (vgl. Beispiel). Ein Würfel lässt sich auch zeichnen.

Ich verstehe jedoch die in der verlinkten Aufgabe aufgeführte Notation der Geraden noch nicht. Weshalb gibt es dort eine weitere Variable u?

Ebenen sind noch nicht dabei. Ich gehe davon aus, dass hier die Angabe von 2 Punkten bzw. 1 Vektor genügt, um die Ebene einzuzeichnen.

---

A₁ ist die Parameterdarstellung einer Ebene.

P(1,2,3) ist der Stützpunkt, (0,1,0) und (1,1,0) sind die Richtungsvektoren. Du kannst ein Parallelogramm in P(1,2,3) anfügen und dann zu einer Ebene ergänzen.

\( _{1}=\left\{\vec{x} \mid \vec{x}=\left(\begin{array}{l}1 \\ 2 \\ 3\end{array}\right)+r \cdot\left(\begin{array}{l}0 \\ 1 \\ 0\end{array}\right)+s \cdot\left(\begin{array}{l}1 \\ 1 \\ 0\end{array}\right)\right\} \)
\( { }_{2}=\left\{\vec{x} \mid \vec{x}=\left(\begin{array}{l}0 \\ 0 \\ 1\end{array}\right)+t \cdot\left(\begin{array}{l}1 \\ 2 \\ 1\end{array}\right)+u \cdot\left(\begin{array}{l}2 \\ 4 \\ 2\end{array}\right)\right\} \)

Bei A₂ ist der zweite Richtungsvektor nur länger als der erste. u*(2,4,2) bringt daher keine weiteren Punkte zu

x = (0,0,1) + t(1,2,1) hinzu.

---

Die Gerade x = (0,0,1) + t(1,2,1) lässt sich bequem zeichnen (einfach zwei Punkte, die auf der Gerade liegen, angeben).

Den Würfel muss man mit exakten Koordinaten angeben.

Wenn ich das Obige richtig interpretiert habe, sieht es jetzt so aus. Jedoch kann ich die Würfelmaße aus o.g. Angaben nicht deuten.

---

Sehr schön. Berechne nun den Schnittpunkt S von g und E. Er liegt auf g.

Du kannst ihn dann wie bei einem Kräfteparallelogramm von deinem P aus anpeilen.

Der Koordinatenquader von S ist dann das, was in einem der Kommentare gestrichelt gezeichnet wurde.

Das dürfte verlangt sein, wenn die Aufgabe gelöst wird.

---

Nun können auch Ebenen via Dreipunkteform eingezeichnet werden.

Beispiel:

Für die obige Aufgabe:

1. Zeichnet man die erste Gleichung (mit "ebene"), so erkennt man, dass nur eine weiße Gerade übrig bleibt.

2. Zeichnet man die zweite Gleichung (mit "ebene"), so erkennt man, dass sich eine Ebene ergibt.

Hier in 3D aufrufen.

Trotzdem kann ich noch nicht den erwähnten Würfel erkennen.

---

Sieht schön aus. Nur: Warum hast du von P aus 3 Pfeile gezeichnet? Der kleine grüne Pfeil zeigt ja aus der Ebene raus? Soll das ein Normalenvektor auf E sein?

Willst du nicht die Gegenstände in der Graphik anschreiben, damit ein Bezug zur Eingabe erkennbar ist? 

" Trotzdem kann ich noch nicht den erwähnten Würfel erkennen.  "

Dazu müsstest du erst den Schnittpunkt der Ebene und der Geraden berechnen und einzeichnen. Nur der hat den gewünschten Koordinatenquader. 

---

Diese beiden kleinen Vektoren waren noch von der Aufgabe, siehe Link oben.

Wenn wir nur die Ebenen zeichnen, sieht die 3D-Abbildung so aus:

Dabei sind die beiden hellroten Vektoren die, die die grüne Ebene aufspannen.

---

Du hast jetzt eine Ebene und eine Gerade eingezeichnet. Das ist übersichtlicher.

Wie kommt |v| = 26.944 zustande?

v scheint der Richtungsvektor der Geraden zu sein. Da kann man etwas mehr als nur Vektor dazuschreiben.

---

|v| = 26.944 ist der Vektor zwischen den beiden angegebenen Vektoren der Gerade. Dachte mir, das könnte eventuell hilfreich sein? Richtungsvektor. 

Was soll noch dazu geschrieben werden? Was soll bzw. kann in die Angaben/Berechnungen zur Ebene mit hinein?

---

Der ist doch v=(1|2|1) und hat keinesfalls eine Länge von über 26 (?)

---

Danke für den Hinweis. Soeben behoben, nun werden die korrekten |v| = 2,449 angezeigt. Es ist der Vektor, der von den beiden Punkten auf der Gerade bestimmt wird.

gerade(0|0|1 1|2|2) → v(1|2|1)

|v| = √6 ≈ 2,449

PS: Welche Berechnungen soll ich noch für die Ebene anzeigen?

---

Update 05.09.2015:

Angeregt von dem Kommentar von Mitglied TR habe ich folgendes ergänzt:

Ebene: Parameterform und Koordinatenform werden nun berechnet und angezeigt.

Gerade: Die Spurpunkte (Achsenabschnitte) werden nun errechnet und als Punkte eingezeichnet.

Koordinatenebenen: Es lassen sich nun die Koordinatenebenen separat einblenden/ausblenden. Die Anzeige kann  mit Eingabe von "koordinatenebenen(xy xz yz)" gesteuert werden, nicht benötigte weglassen.

Die dazugehörigen Beispiele findet ihr hier.

---

Update: Ich habe den Geoknecht um ein Rotations-Feature ergänzt. Syntax würfel(0|0|0 3)[0 0 45].

Text ist nun in x-y-z-Richtung drehbar. Beispiel hier.

Der Würfel ist rotierbar. Beispiel hier.

Der Quader ist rotierbar. Beispiel hier.

Damit wird das 3D-Programm noch leistungsfähiger!

Welche Objekte sollten noch rotierbar sein?

Gruß Kai

---

Separate News-Meldung herausgegeben:

Geoknecht 3D: Rotationen + neuer Zylinder + Wertänderungen für Animationen

Geoknecht gibt es jetzt auch auf Englisch. Dort heißt das Programm: Geoservant 3D

---

Update 17.09.2015 (v1.13):

1. Vektoren waren stets mit zwei Punkten anzugeben. Jetzt könnt ihr sie nur mit einem Punkt (also 3 Komponenten) angeben, dann wird als Startpunkt der Koordinatenursprung gezeichnet. Vorher: vektor(0|0|0 2|3|2) Neu: vektor(2|3|2).

2. Vektoren können nun auch mit Labeln versehen werden. Beispiel Vektoraddition hier.

Zusatz: Performance verbessert. Das Rendering erfolgt nur, wenn eine Wertänderung stattfindet. Vorher war es noch bei jedem KeyUp.

---

Update (Version 1.14):

- Vektoren werden nun mit Startpunkt und Vektor eingegeben
- wird der Startpunkt bei der Eingabe weggelassen, so wird der Koordinatenursprung als Startpunkt gesetzt, Beispiel 
- der Winkel zwischen Vektor und xy-Ebene wird nun zusätzlich berechnet, Beispiel 
- bei Eingabe von # am Ende der Vektorzeile erscheinen Hilfslinien, Beispiel
- der Spat (Parallelepiped) ist nun verfügbar! 
- für den Spat werden stets Oberfläche und Volumen berechnet (sehr hilfreich zur Überprüfung - Beispiel hier) 

Zusatz: Geoknecht Versionsnummer rechts unter der 3D-Szene hinzugefügt

---

Update (Version 1.17):

Per Copy & Paste eingefügter Text wird nun gefiltert und ggf. umgewandelt:

1. Alle / werden zu |.

2. Alle unnötigen Leerzeichen vor und hinter Klammern werden entfernt.

3. Eine eingefügte Zeile mit A(0|4|2) wird umgewandelt zu punkt(0|4|2 "A")

Unsaubere Eingabe via Einfügen: A ( 3 / 2 / 1 ) wird automatisch bereinigt zu: punkt(3|2|1 "A")

---

Die Umwandlung erleichtert natürlich die Eingabe.

Kann man somit keine Koordinaten exakt in Bruchform eingeben?

Test mit

A( 1/3 | 0 |3)

B(√2 | 3| 8)

---

Brüche umwandeln würde im Widerspruch zur Komplettumwandlung von / zu | stehen. Man bräuchte schon einen ausgefeilten Parser, um das richtig zu interpretieren.

Wurzel ist zu überlegen, aber dann ist wieder die Frage nach der korrekten Eingabe. Wenn jemand wirklich nur das Wurzelzeichen gefolgt mit nur einem Zahlenwert eingibt, dann wäre das ggf. möglich. Ansonsten bitte die gerundeten Werte eintragen. Für √2 sollte als Genauigkeit der Zeichnung ≈ 1,414 genügen.

---

Update (Version 1.18): 

Ihr könnt nun die Farben der Körper (auch Texte und Vektoren) selbst bestimmen. Hierzu einfach die Hex-Farbcodes am Ende mit geschweiften Klammern anhängen.

Beispiel: Roter Quader mit quader(0|1|0 4 2 1){F00}

Weiterhin neu: Statt ALT+Pfeiltasten zur Wertänderung ist jetzt der Shortcut STRG+SHIFT+Pfeiltasten zu nutzen. Grund ist, dass im Browser Chrome mit ALT ←  manchmal auf die vorige Seite zurückgesprungen wurde.

---

Update (Version 1.19): 

Es lassen sich Halbkugeln und Teilkugeln erzeugen.

Beispiel: kugel(0|0|4 4 0 6.28 1.55 3.14)

Die englische Version "Geoservant 3D" greift nunmehr auf die gleiche Bibliothek zu wie die deutsche Version.

Zusätzlich 3D-Galerie erweitert.

---

Video: "Geoknecht 3D - Revolution für den Mathe-Unterricht (3D Geometrie)"

https://www.youtube.com/watch?v=OupOoi_lRw4

Wir begannen die Entwicklung des Programms Geoknecht 3D vor 1,5 Jahren. Nun ist er in voller Funktion fertiggestellt und steht euch allen uneingeschränkt zur Verfügung: https://www.matheretter.de/geoservant/de

Mit dem Geoknecht könnt ihr geometrische Körper sehr einfach mit Text erstellen. Zum Beispiel würfel(0|0|0 5)`eintippen und es wird ein Würfel im Koordinatenursprung mit der Kantenlänge 5 angezeigt. Die verfügbaren Zeichenobjekte sind: Dreieck, Ebene, Gerade, Kugel, Polygon, Punkt, Quader, Spat, Strecke, Text, Vektor, Viereck, Würfel, Zylinder.

Mit dem Geoknecht könnt ihr:

- Objekte erstellen (und automatisch berechnen)

- Objekte animieren

- Objekte rotieren

- Objekte einfärben

- alle Koordinatenebenen einblenden bzw. ausblenden

- Variablen festlegen

Soweit die News.

---

Kann ich hier noch auf eine bessere Schrägbildzeichnung kommen?

https://www.matheretter.de/geoservant/de?draw=punkt(3%7C0%7C1%20%22A%22)%0Apunkt(3%7C6%7C3%20%22A'%22)%0Apunkt(0%7C0%7C4%20%22B%22)%0Apunkt(3%7C3%7C2%20%22P%22)%0Apunkt(6%7C6%7C0%20%22B'%22)%0Avektor(0%7C0%7C0%203%7C0%7C1)%0Avektor(0%7C0%7C0%203%7C6%7C3)%0Avektor(0%7C0%7C0%200%7C0%7C4)%0Avektor(3%7C0%7C1%200%7C3%7C1)%0Avektor(3%7C3%7C2%200%7C3%7C1)

Die Skizze erweckt den Eindruck AP und PA' seien nicht gleich lang.

Betrifft https://www.mathelounge.de/427254/wie-komme-ich-bei-dieser-aufgabe-auf-den-spiegelpunkt-nr-6-0-0?show=427256#a427256

---

Update 07.12.2017:

Ihr könnt jetzt auch die Transparenz eines geometrischen Körpers separat festlegen. Einfach hierzu eine geschweifte Klammer am Ende ansetzen mit dem Transparenzwert (zwischen 0 und 1).

Oder global die Transparenz bestimmen, siehe kleines Eingabefeld unterhalb des 3D-Fensters.

---

Die Änderungen von 2016 bis 2020 habe ich nicht getrackt. Wir sind nunmehr bei Version 1.55 angelegt.

Eine Gesamtübersicht aller Funktionen findet man jedoch immer unterhalb des Geoknecht-Fensters selbst: https://www.matheretter.de/geoservant/de

Update vom 12.01.2021:

1. Checkboxen für Koordinatenebenen gesetzt.
2. Punkte können nun gefärbt werden.
3. Klick auf camera(1|2|3) rechts wandelt dieses nun in ein Inputfeld um, damit ist es leichter zu kopieren.
4. Änderung der Schriftgröße bei text und punkt möglich.

Die manuelle Eingabe der Koordinatenebenen bleibt weiterhin gewährleistet. Sie wird sogar vorrangig behandelt. Auch nur dort kann man das Gitternetz je Ebene separat an- und ausschalten.

Das heißt, koordinatenebenen(xy xz yz) hat Vorrang vor den Checkboxen. Diese werden im Übrigen ausgeblendet, sofern solch eine Eingabe existiert.