Berechne, den Abstand der Leiter (Tangente an Heuhaufen) vom Heuhaufen f (x) = 3x - 0,5x^2 auf dem Boden.

Question

die obere berandung eines heuhaufens lässicht sich näherungsweise durch die funktion f mit f (x) = 3x - 0,5x^2 (x und f(x) in m) beschreiben. im punkt p (4/f(4)) soll tangential eine leiter angelegt werden.

Klausurvorbereitung

Answer 1

Hi Kai,

 

Bestimme die Ableitung im Punkt P, was der Steigung der Tangente entspricht.

f'(x)=3-x

f'(4)=-1

 

Die allgemeine Tangente hat die Form y=mx+b.

m wurde dabei gerade zu m=-1 bestimmt.

 

Nun noch den Punkt P(4|f(4)) -> P(4|4) einsetzen:

4=-4+b -> b=8

 

Die Tangente lautet t(x)=y=-x+8

 

Wir haben also nun die Tangente und die Funktion, welche den Heuhaufen beschreibt. Von beiden den Abstand zu berechnen, fordert die Nullstellen von beiden zu bestimmen:

t(x)=-x+8=0 -> x=8

f(x)=3x-0,5x^2=0 -> x₁=0 und x₂=6

 

Der Abstand von Heuhaufen und Leiter ist also 8-6=2.

Im Schaubild verdeutlicht:

 

 

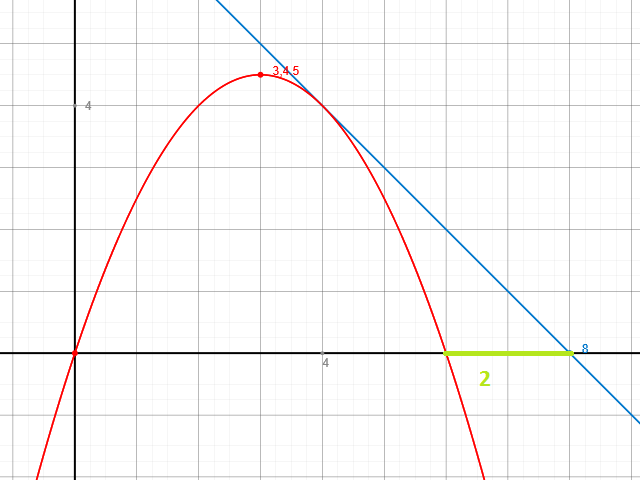
Grüße