Also ich habe die Seitenlängen einfach erst mal mit Pythagoras ausgerechnet. Oder ist Pythagoras nicht erlaubt? Naja, ich stelle meine Lösung trotzdem einfach mal vor. ^^
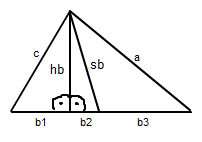
Man weiß:
b1 + b2 + b3 = 6,25
Und b3 ist genau die Hälfte von b, das erkennt man ja an der Seitenhalbierenden sb. Also:
b3 = 3,125
und b1 + b2 = 3,125
b2 kann man mit Pythagoras in dem Dreieck mit den Seiten b2, hb und sb berechnen.
hb² + b2² = sb²
5,12² + b2² = 5,57²
b2² = 5,57² - 5,12²
b2 = √(5,57² - 5,12²)
b2 = √4,8105
Nun kann man daraus auch b1 berechnen.
b1 = 3,125 - b2 = 3,125 - √4,8105
Dann hat man jetzt alle einzelnen Teile der Seite b und kann nun mit Pythagoras auch an a und c kommen.
(b2 + b3)² + hb² = a²
(√4,8105 + 3,125)² + 5,12² = a²
a = √((√4,8105 + 3,125)² + 5,12²) ≈ 7,382
b1² + hb² = c²
(3,125 - √4,8105)² + 5,12² = c²
c = √((3,125 - √4,8105)² + 5,12²) ≈ 5,204
Die Winkel lassen sich, wenn man die entsprechenden Seitenlängen hat, ja einfach mit Sinus etc. berechnen, z.B. so:
α = tan-1(hb / b1) = tan-1(5,12 / (3,125 - √4,8105)) ≈ 79,686°
γ = tan-1(hb / (b2 + b3)) = tan-1(5,12 / (√4,8105 + 3,125)) ≈ 43,912°
β ≈ 180° - 79,686° - 43,912° ≈ 56,402°