Zunächst einmal die Skizze
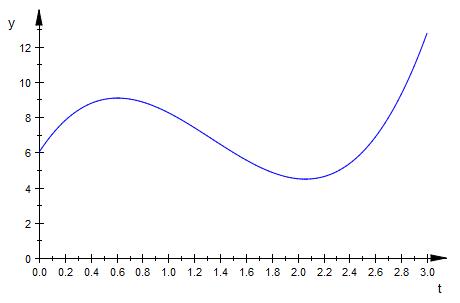
Ein Gartenteich ändert seinen Wasserstand im Sommer fortwährend
aufgrund von Hitze und Regenfällen. Das Wasservolumen im Teich kann
näherungsweise beschrieben werden durch die Funktion V mit
V(t) = 3t3 - 12t2 + 11,25 t + 6 ( V ist das Volumen im km3, t die Zeit in Tagen, 0 < t < 3).
km^3 wäre ein bißchen viel. 12 km^3 sind 12 Kubikkilometer. Ich vermute m^3.
a) wann ist die Zulaufgeschwindigkeit im betrachteten Zeitintervall [-0,5; 3,5]
am größten? Begründe rechnerisch.
Das Intervall geht über die vorherige Angabe 0 < t < 3 hinaus !!!
Zulaufgeschwindigkeit = Steigung
Größte Zulaufgeschwindigkeit ist am Wendepunkt von V.
V ´ ( t ) = 9 * t^2 - 24 * t + 11.25
V ´´( t ) = 18 * t - 24
Wendepunkt
18 * t - 24 = 0
t = 1 1/3
Der Wendepunkt ist im Bereich in dem die Ablaufgeschwindigkeit
am größten ist.
Wir müssen also die Geschwindigkeit bei x = -0.5 und x = 3.5
berechnen.
V ´( -0.5 ) = 25.5 m^3 / Tag
V `( 3.5 ) = 37.5 m^3 / Tag
b) Bestimme die Zeitpunkte, in denen die Ablaufgeschwindigkeit -1,5km3
pro Tag beträgt.
V ´( t ) = -1.5 m^3 / Tag
9 * t^2 - 24 * t + 11.25 = -1.5
Mitternachtsformel oder
pq - Formel oder
quadratische Ergänzung
Zur Kontrolle : t = 0.73 und t = 1.93
Schaffst du das ?
Bin bei Bedarf gern weiter behilflich.