Hi Bertel,
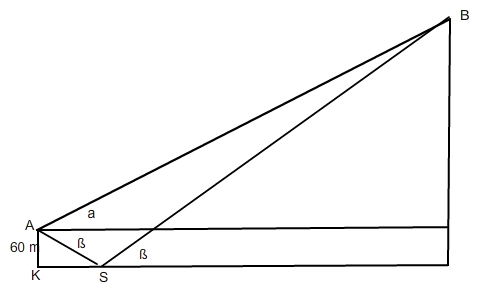
nimm den Koordinatenursprung und berechne die Strecke zu S: tan(53,4°)*60m=80,79m.
Nun kannst Du zwei Geraden aufstellen:
(Gerade von A nach B) y=tan(31,6°)*x+60
(Gerade von S nach B) y=tan(36,6°)*x-60
(die -60 ergeben sich, wenn man S einsetzt).
Nun nur noch gleichsetzen:
tan(31,6°)*x+60=tan(36,6°)*x-60
x=639,2
Der Berg hat also eine Höhe von 639,2 m über dem See.
Grüße