Question

Kann man berechnen wan ein Auto das andere überholt ohne zu wissen wie lange die Autos sind?

lG Andrin

Answer 1

Kann man berechnen wann ein Auto das andere überholt, ohne zu wissen wie lang die Autos sind?

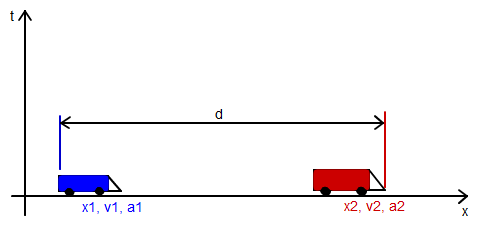
Nach dem allgemeinen Verständnis würde man sagen, das blaue Auto hat das rote Auto überholt, wenn die hintere Stoßstange vom blauen Auto auf der Höhe der vorderen Stoßstange des roten Autos ist bzw. schon daran vorbei. Das ist dann der Fall, wenn d = 0 ist. d ist dabei der Abstand zwischen zwischen dem hinteren Ende des blauen Autos und dem vorderen Ende des roten Autos.

Wenn man nun v1, a1 und v2, a2 und d kennt, kann man den Zeitpunkt errechnen, an dem der Überholvorgang abgeschlossen ist. Wenn man also dieses d(t=0) kennt, dann braucht man nicht die Länge der Autos zu kennen.

Es gilt:

x₂ = 1/2*a₂*t^2 +v₂*t +x_0,2; //Bewegungsgleichung für gleimäßig beschleunigte Bewegung
x₁ = 1/2*a₁*t^2 +v₁*t +x_0,1;
d(t) = x₂ -x₁ = 1/2*a₂*t^2 +v₂*t +x_0,2 -[1/2*a₁*t^2 +v₁*t +x_0,1] =
     = t^2*(a2 -a1)/2 +t*(v₂ -v₁) +(x_0,2 -x_0,1);

d(t=0) = (x_0,2 -x_0,1);

d(t) = t^2*(a2 -a1)/2 +t*(v₂ -v₁) +d(t=0);

 

Mit der Überholbedingung d(t) = 0:

t^2*(a2 -a1)/2 +t*(v₂ -v₁) +d(t=0) = 0;

abc-Formel für das Lösen quadratischer Gleichungen kann man dann t bestimmen.

 

lg JR