Elferprobe im Dezimalsystem

Question

Aufgabe:

a) Erliautern Sie: Für \( k \in \mathbb{N} \) gilt \( \left[10^{k}\right]_{11}=\left[(-1)^{k}\right]_{11} \)

b) Erläutern Sie: Für Ziffern \( a_{0}, a_{1}, \ldots, a_{m} \in\{0, \ldots, 9\} \) gilt für die Restklasse \( [n]_{11} \) der Zahl \( n=a_{m} \cdot 10^{m}+\cdots+a_{1} \cdot 10+a_{0} \) dass \( [n]_{11}=\left[(-1)^{m} a_{m}+\cdots-a_{1}+a_{0}\right]_{11} \)

c) Erläutern Sie: \( 11 | n \) genau dann wenn \( 11 |(-1)^{m} a_{m}+\cdots-a_{1}+a_{0} \)

d) Überprüfen Sie mithilfe der Elferprobe, ob die im Dezimalsystem angegebene Zahl 864202468 durch 11 teilbar ist.

Ich brauche Hilfe bei Elferprobe im Dezimalsystem.

Comments

Kannst du mit den Beispielen hier : https://de.wikipedia.org/wiki/Neuner-_und_Elferprobe#Rechenbeispiele

vielleicht etwas basteln? 

Answer 1

auch wenn diese Frage schon sehr lange her ist, möchte ich sie nun 1.5 Jahre später beantworten:-)

(a) Es ist \(10\equiv -1\mod 11\), denn \(10+t\cdot 11\text{ mit } t=-1\) ist \(10-1\cdot 11=-1\). Es ist also \((10)^k=(-1)^k\).

(b) Die Grundlage für unsere Argumentation haben wir bereits in (a) geschaffen. Die im Aufgabentext verwendete Darstellung von \(n\) erwähne ich zudem in (c). Man verwendet folgende Äquivalenz: \(10^m \equiv (-1)^m\mod 11\), also \(n=a_m\cdot 10^m \equiv a_m\cdot (-1)^m\). Es ist außerdem \(a_0\cdot (-1)^0 = a_0\cdot 1=a_0\) positiv und \(a_1\cdot (-1)^1=a_1\cdot (-1)=-a_1\) negativ.

(c) Das ist das Teilbarkeitskriterium für 11: "Eine Zahl ist genau dann durch 11 teilbar, wenn ihre Wechselsumme durch 11 teilbar ist".  Hier wurde der in (a) erläuterte Umstand ausgenutzt, dass \(10\equiv -1\mod 11\). Eine alternative Darstellung wäre: 

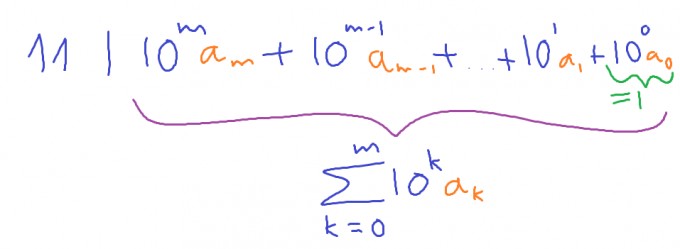
Da die obige Darstellung die Zahl \(a_ma_{m-1}...a_1a_0\) im Dezimalsystem repräsentiert und die im Aufgabentext verwendete Schreibweise dazu äquivalent bezüglich des Moduls 11 ist, kann mit dieser Probe eine Zahl auf die Teilbarkeit durch 11 getestet werden.

(d) Hier soll die in (c) erläuterte Elferprobe angewendet werden:

 

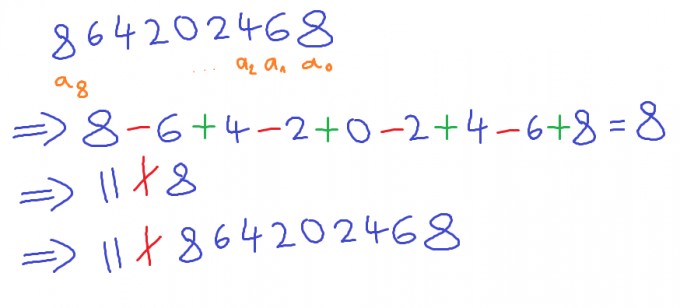
Hast Du die Aufgabe eigentlich noch lösen können?

André, savest8