Funktionsterm für Übergang zwischen Gleisen

Question

Zwei parallel verlaufende Eisenbahngleise sollen miteinander so verbunden werden, dass man von einem zum anderen wechseln kann.

Angenommen die jeweils linken Gleise haben einen Abstand von 5 Metern und zwischen ihnen soll in einer Länge von 100 Metern ein Übergang hergestellt werden. Bestimme den Funktionsterm des Graphen, der den Übergang zwischen den beiden beschreibt.

Answer 1

Für die verbindene Funktion  gilt

f ( 0 )  = 5
f ( 100 ) = 0
f ´ ( 0 ) = 0
f ´( 100 ) = 0

4 Aussagen  => Funktion 3.Grades

f ( x ) = a * x^3 + b * x^2 + c * x + d

f(x) = 1/100000·x^3 - 0,0015·x^2 + 5

~plot~ 1/100000 * x^3 - 0.0015 * x^2 + 5 ; [[ 0 | 100 | 0 | 5 ]] ~plot~

Comments

Könntest du nochmal erklären wie auf diese 4 Aussagen kommst?

---

Es sind einige Angaben meiner Meinung nach nicht gegeben

- die Gleisbreite

Mitgeteilt wurde icht ob die Anschlustellen knickfrei sein sollen.
Davon gehe ich aber aus.

Knickfrei heißt : die beiden Gleise und das Verbindungsstück
haben in den Anschlußpunkten dieselbe Steigung.

Mein mathematisches Modell sieht so aus

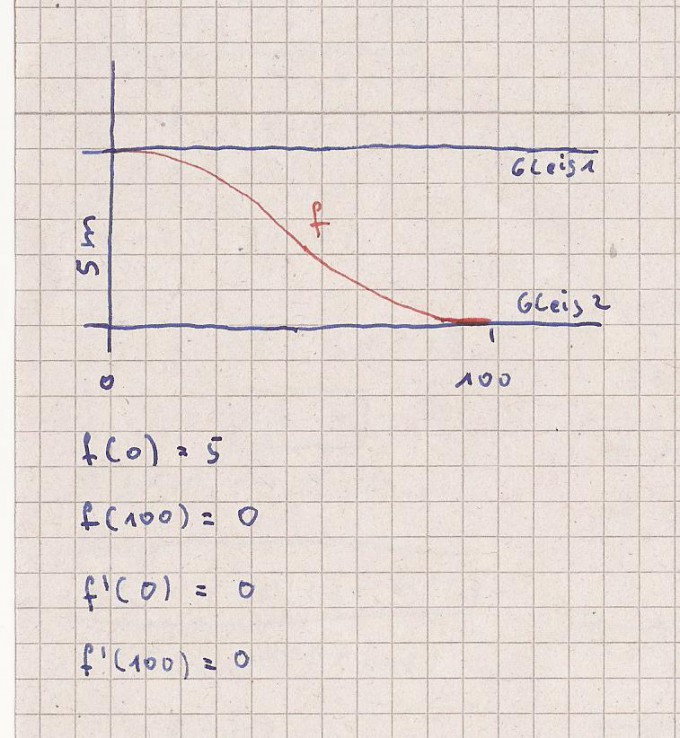
Die " Steigung " der beiden Gleise ist überall null.

Die erste Ableitung  f ´der Funktion soll in den Anschlußpunkten
dieselbe Steigung haben..

Eine Parabel als Funktion 2.Grades passt nicht, weil nur der Scheitelpunkt
die Steigung 0 hat ( nur 1 Punkt ).

Die nächste Funktion wäre eine Funktion 3.Grades.

f ( x ) = a * x^3 + b * x^2 + c * x + d

Wir haben 4 Gleichungen und 4 Unbekannte. Eine Lösung
sollte möglich sein.

Bei Fragen wieder melden.